תורת הכדורים (כבידה קוונטית)
או ריק חסר ממדים – כחזות הכול (אוגוסט – 2017 – עדכונים: מאי – 2022, ינואר, אפריל ונובמבר 2024 ועדכון אחרון אפריל – 2025)
(קוונטים – כוח הכובד, חומר אפל/אנרגיה אפלה ….)
ערן שמעוני
פיסיקאי (B.sc.), מנהל עסקים (MBA) ושמאי מקרקעין
הקדמה:
מגיל צעיר מאוד העסיקה אותי השאלה איך נוצר ועובד העולם שסביבנו. וכשאלת מישנה האם התשובה, בשבילי, ראוי שתבוא מעולם המדע או מעולם הדת ("אלוהים"/"כוח עליון"). לצורך מציאת תשובות, כילד, הלכתי לחוגי העשרה, בפיסיקה ובאסטרונומיה, ב"מכון וויצמן למדע", ברחובות וב"מצפה הכוכבים בגבעתיים" ו"בלעתי" את ספרי הפיסיקה שהיו זמינים, אז, בעברית, כולל תרגומים של ספריו הראשונים של המדען "סטיבן הוקינג".
מאוחר יותר, וטרם הגיוס לצבא, המשכתי, במקביל, לחפש את התשובה לשאלה גם בעולם הדת. במשך מספר שנים בילית בקורס לחוזרים בתשובה בהדרכת רב שבעצמו חזר בתשובה שנים קודם לכן. ואף, לאחר השחרור, הלכתי למספר הרצאות בקבלה. מהקורס והקבלה הסקתי שלמרות שלא קיבלתי תשובה לשאלת קיומו או אי-קיומו של ה"אלוהים", התשובה לשאלה איך נוצר ועובד העולם, בשבילי, לא תבוא מעולם הדת. והחלטתי להירשם ללימודי הפיסיקה לתואר הראשון ב"אוניברסיטה העברית".
במשך לימודי התואר, ראשית בשביל עצמי, בניסיון לענות על שאלת מקור העולם, התחלתי לחשוב על כתיבת מאמר קצר.
עם הזמן, לאחר שנים שהעליתי ופסלתי רעיונות אחרים, עלה רעיון אופציית הכדורים.
משהתחלתי להעלות על הכתב את הפרקים הראשונים, לפני יותר מעשרים שנה, התגלו סתירות רבות שאילצו אותי לשנות שוב ושוב. עם התגבשות רעיון הכדורים, בצורתו הכמעט סופית, התברר כי קיימות בו סתירות, לפחות לכאורה, עם חלק ממוסכמות היסוד בעולם הפיסיקה, לדוגמה: ההנחה שמהירות האור היא מהירות קבועה, תאוריית ה"מפץ הגדול" להתפתחות היקום ועוד.
רק בשנת 2017 סיימתי את כתיבת הגרסה הראשונה של החלק הראשון (א') של המאמר. גרסה שכמובן עברה ועוברת שינויים ותוספות מאוחרות יותר. מכאן הכתיבה רק הלכה וצברה תאוצה.
בעקבות תגובות וביקורות, לאחר קריאה, של חברים ומדענים, נוספו עוד ועוד פרקים. כך שניראה שבמצבו הנוכחי המאמר מציע תורת כבידה (גאומטרית) קוונטית לאיחוד כוח הכובד עם הכוחות האחרים הקיימים בטבע וכן תאוריה כללית למבנה הייקום העוסקת בהיווצרותו ובאבולוציה שלו.
"תורת הכדורים", מעבר להיותה תאוריית כבידה קוונטית, מצליחה בהסבר תופעות נוספות כגון: החומר והאנרגיה האפלים, השתנות מהירות האור בזמן, המושג מסה, יצירת פוטונים, מוליכות על ועוד.
חלק א: בסיס התורה
פרק 1: כוח הכובד
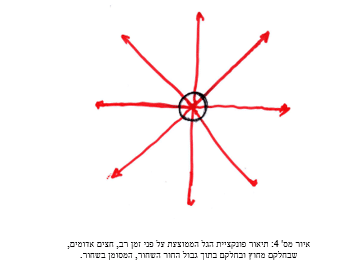
כידוע היום, מרבית נפח היקום הינו ריק כמעט מוחלט, כזה עמוק, שלא ניתן להשיגו, על פני כדור הארץ, באמצעים הטכנולוגיים הזמינים. מכאן ניתן, בנקל, לתאר את החלל כמרחב רב מימדי המורכב, מרביתו, מנקודות ריק כמעט מוחלט (נקודות בשחור, איור מס' 2), התופסות כל אחת מהן נפח קטן עד כדי מימדים השואפים לאפס.
עתה נניח כי כל נקודה כזאת מוקפת, מכול עבר, באין ספור נקודות דומות ונתייחס לתורת הקוונטים הקובעת, בין היתר, כי:
- למסה, גם כזו השואפת ל- 0, מוצמדים תדירות עצמית ואורך גל אופייניים.
- ככול שהמסה קטנה יותר (מימדים קוונטיים) אורך הגל האופייני ארוך יותר.
- ככול שהמסה גדולה יותר אורך הגל האופייני קצר יותר, עד שהופך להיות חסר משמעות בגדלים שאינם קוונטיים.
.
משהנחנו שכל אחת מהנקודות מהווה ריק כמעט מוחלט במסה קטנה מאוד, עד כדי שאיפה לאפס, מתקבל, בשילוב ההתייחסות לתורת הקוונטים (נקודה שנייה), כי אורך הגל האופייני לנקודה גדול מאוד, למעשה, שואף לאין סוף. ניתן לתאר (איור מס' 1) אורך גל זה, היוצא מהנקודה כלפי חוץ לכול הכיוונים ובכל המימדים האפשריים, כדוחף את המרחב החיצוני לנקודה. דבר היוצר דחייה מהנקודה והלאה, (להל"ן: "עיקום המרחב שיוצרת הנקודה").

עתה נציע טרנספורמציה מתמטית מוכללת לסיכום ווקטורי, כך ש"טרנספורמציית לורנץ" לסיכום מהירויות תהיה מקרה פרטי שלה, ושסיכום כל ווקטורי עיקומי המרחב שיוצרות כול הנקודות סביב נקודה כלשהי במרחב לפיה ייתן, בכל אחד מהכיוונים והמימדים האפשריים, עוצמה שלכול היותר תהיה כעוצמת עיקום המרחב שיוצרת נקודה אחת, שווה לעוצמה זו כשהמדובר באין סוף נקודות. דוגמה להכללה ל"טרנספורמציית לורנץ": נניח שאנו נעים במהירות האור על גבי רכבת שנעה במהירות האור שבתורה נעה על רכבת שגם היא נעה במהירות האור וחוזר חלילה n רכבות כאלו (n – שואף לאין סוף) עד לרכבת הראשונה. נובע מהכללה ל"טרנספורמציית לורנץ" ומהעובדה שמהירות האור היא המהירות המקסימאלית האפשרית שהמהירות שלנו יחסית לכדור הארץ (n רכבות) תהיה לא יותר ממהירות האור עצמה וקרובה לה.

משנסכם, בעזרת הטרנספורמציה המתמטית שנוצרה, את ווקטורי עיקומי המרחב שיוצרות כול הנקודות סביב עם עיקום המרחב שיוצרת הנקודה הנבדקת עצמה מנגד, כל עוד מסתה שואפת ל- "0", ובהנחה של פיזור הומוגני של אין סוף נקודות במרחב שסביבה, נקבל כי הווקטורים יאזנו זה את זה, כך שנטו השפעת המרחב על הנקודה הנבדקת תתקזז עם השפעת הנקודה מנגד, והמערכת תהיה ב"שיווי משקל רופף".
מכאן הדרך ליצירת פוטון, חופשי, בעל אנרגיה וללא מסה קצרה. דיון מורחב, מעט יותר, בפוטונים ותנועתם בפרק 28, בחלק השני של המאמר.
נבדוק את סיכום ווקטורי המרחב והנקודה הנבדקת עצמה במקרה שמסתה הולכת וגדלה עד למימדים שאינם קוונטיים (איור מס' 3). במקרה כזה אורך הגל של התדירות העצמית של הנקודה "קטן", עד שהופך להיות חסר משמעות במסה שאיננה מסדר גודל קוונטי (ראה ההתייחסות לתורת הקוונטים נקודה שלישית, בתחילת הפרק). ובכך, לאחר שתיארנו את אורך הגל כדוחף את המרחב, יורדת גם עוצמת עיקומה את המרחב (איור מס' 3, בכחול). מתקבל כי סיכום ווקטורי עיקום המרחב שיוצרות כול הנקודות סביב, קבוע שאיננו תלוי בנקודת המסה (איור 3, באדום), גובר על עיקום המרחב ה"מוקטן" שיוצרת המסה עצמה מנגד. כך שסה"כ סיכום ווקטורי עיקום המרחב נטו, מכל הכיוונים ובכל המימדים האפשריים, הוא חיובי לתוך המסה והמסה מאין "מוחזקת" ע"י המרחב ב"שיווי משקל יציב". בדומה להגדרה הקלאסית למסה – "התנגדות של גוף לשינוי מצבו".

כך אנו רואים כי במקרה של מסה שאיננה אפסית, תורת הקוונטים עצמה, בשילוב "תורת הכדורים", חוזה כי ייווצר עיקום של המרחב לעבר המסה. כל זאת בדיוק כפי שחוזה תורת היחסות הכללית, המסבירה בכך את קיומו של כוח הכובד.
פרק 2: חומר אפל/אנרגיה אפלה
(בפרק זה, אין הכוונה למושג "אנרגיה אפלה", כפי השגור בפי הדוגלים בתיאוריית ה"מפץ הגדול", המכוון לאנרגיה הנעלמת הנחוצה להאצת היקום, כפי שנצפה. נושא עליו נרחיב, מעט, את הדיון בסוף פרק 11, סעיף "לאחר הניסוי" ובפרק 46 בסוף החלק הרביעי של המאמר)
עד אתה נגעתי בקשר בין תורת הקוונטים וכוח הכובד. אתה אדון בפן נוסף הנובע מהתדירות העצמית של גדלים קוונטיים. וידוע כי בהינתן גוף בעל מסה ניתן בנקל לחשב את התדירות העצמית ואורך הגל האופייני לו (משוואת הגלים) אשר, כפי שאמרנו כבר קודם, ככול שנתייחס לגדלים קוונטיים, יהיה גדול יותר.
לצורך הדוגמה נתייחס לנקודת ריק כמעט מוחלט/"חור שחור" בו חלק "מפונקצית הגל" יכול, בממוצע על פני זמן רב, שתהיה מחוץ לגבולות החור השחור (להלן: "אפקט המנהרה" או "התאדות של חור שחור").
נגדיר את "כמות החומר" כפונקציה של החלק הנצפה של "פונקצית הגל" וב"חור השחור" שבדוגמה נניח אורך גל ותדירות עצמית כאלו כך שחלק מפונקצית הגל, לצורך העניין 90% בממוצע לאורך זמן, נמצאת מחוץ לגבולות החור השחור. מתקבל כי צופה שבתוך אופק הארועים של החור השחור, בשל הקביעה, העולה מתורת היחסות הפרטית, שמהירות האור היא סופית והמקסימאלית האפשרית, ימדוד רק את כמות החומר הפרופורציונאלית ליתרת פונקצית הגל, 10% בממוצע לאורך זמן, בעוד המסה אותה ימדוד תהיה אותה המסה, המרוכזת במרכז הכובד, הכוללת את זו שבממוצע לאורך זמן מחוץ ובתוך החור השחור, יחדיו.
נותר רק להניח שהיקום הידוע כולו הוא חור שחור כדוגמת זה שתואר ומתקבל כי אנו, אותם צופים החיים בפנים, רואים מסה ללא הצמדה של חומר/אנרגיה (להלן: "חומר אפל"/"אנרגיה אפלה").
נראה, שאין ביכולת פרק זה לספק הסבר מלא לכלל תופעת החומר האפל. הסבר אפשרי נוסף, טוב לא פחות לתופעה, המתבסס על תאוריית היקומים התאומים, בפרק 39, שבחלק הרביעי של המאמר.
פרק 3: צופה חיצוני לחור השחור
צופה הנמצא מבחוץ מודד רק את כמות החומר הפרופורציונאלית לחלק פונקציית הגל שנמצאת בממוצע לאורך זמן מחוץ לחור השחור, בדוגמה 90%, בעוד המסה שימדוד תהיה אותה המסה שמודד הצופה מבפנים. חומר זה יתפזר במרחב החיצוני לחור השחור, ללא כיוון מועדף ובמידה שווה לכל הכיוונים, כך שבכל נקודה השפעתו תהיה זעירה עד מאוד.
סיכום ההשפעות הווקטוריות של פונקציות הגל של כל מרכיבי היקום (חורים שחורים, מסות וריקים) על נקודה במרחב, בהנחה של פיזור הומוגני, ייתן את "כמות החומר/רמות האנרגיה האופייניים (E = M x C2) של הריק", אשר תהיה פרופרציונאלית לכמות החומר ביקום.
לו היינו מקטינים את מימדי החור השחור לכדי גודלה של יחידת האנרגיה/מסה, המינימאלית האפשרית, קוונט אחד בלבד, נקבל כי כמעט 100% מפונקציית הגל, לאורך זמן, תהייה מחוץ לחור השחור. קוונט זה יתפזר בכל המרחב האין סופי חסר המימדים (ראה פרק 12: על מגבלת המימדים והיווצרות הקוונטים), החיצוני לחור השחור, בצורה הומוגנית, ללא כיוון מועדף ובמידה שווה לכל הכיוונים. דהינו: הוא יהיה כולו ואף חלק מימנו, בעת ובעונה אחת, בכל מקום במרחב שהוגדר. כך, מכשיר מדידה שימקם את הקוונט במיקום כלשהו או במהירות כלשהי במרחב המוגדר, למעשה, משל היותו יחידת האנרגיה/מסה המינימלית האפשרית, יבטל את האפשרות למציאתו (מדידתו), באותו זמן, בכל מקום אחר.
מתקבל כי שתי מדידות שונות, בזמנים ובמרחקים הסותרים לכאורה את העיקרון כי מהירות האור היא המהירות הגבוהה ביותר האפשרית, העומד בבסיס תורת היחסות הפרטית, לא יהיה בהם עוד סתירה, שהרי הקוונט היה, מאז ומעולם, כולו ואף חלק מימנו, בשתי הנקודות הנבדקות (הסבר מעט מפורט יותר, מנקודת מבט שונה, בהמשך ובעיקר בפרק 22, בחלק השני של המאמר).
פרק 4: זמן/גיל היקום
לצורך חקירת המושג "זמן" נתחיל בכך שנדגיש, את שהזכרנו כבר קודם, כי אורך הגל והתדירות האופיינית לכל נקודה הינם ערכם הממוצע על פני זמן רב (להלן: "נקודת שיווי המשקל"). כך הצעד המתבקש הבא יהיה להניח שקיימות תנודות (אוסילציות) הרמוניות של פונקציית הגל, סביב נקודת שיווי המשקל שלה (להלן: "נקודת שיווי משקל יציב"). לצורך פשטות הדיון נניח כי אנו חיים ביקום (יחידת מסה) חד מימדי, בעל מימדים קוונטיים או שאינם קוונטיים, בו אורך הגל הממוצע על פני זמן רב, הוא כפולה שלמה של מספר גדול מאוד של יחידות מרחק יסודיות (להלן: "יחידת אורך יסודית").

בנקודת זמן אקראית נמדדה פונקציית הגל בתנודה (אוסילציה) בת x יחידות אורך יסודיות, ימינה (החוצה) או שמאלה (פנימה) מנקודת שיווי המשקל (איור 5, חצים אדומים תחתונים). מהיותה של נקודת שיווי המשקל נקודת שיווי משקל יציב, סטטיסטית סביר כי במדידות הבאות תנודת פונקציית הגל תשאף לחזור אליה (איור 5, חצים אדומים עליונים) – אך עדיין, בכל נקודה ברור שקיימות גם אפשרויות סבירות פחות עליהן נרחיב מעט בהמשך, בפרק מס' 41.
כיוון שעפ"י תורת היחסות "מהירות האור" (נסמן ב- "C") היא מהירות החזרה המקסימאלית האפשרית, זמן החזרה לנקודת שיווי המשקל, מנקודת מבטו של הגל הנע במהירות הקרובה למהירות האור, בהנחה של תנועה רגעית במהירות קבועה, יהיה בקירוב, t (יחידות זמן) = C (ק"מ/שניה) / X (יחידת אורך) – (t להלן: "יחידת זמן יסודית").
זמן חזרה זה וכן משרעת התנודה, כפי שימדדו ע"י צופה נח שלא על פונקציות הגל, בהתאם לתחזית תורת היחסות יהיו ארוכים הרבה יותר (הזמן שימדוד יהיה אולי מעבר ל- 14 מיליארד שנה (פרדוקס התאומים), גיל היקום הידוע המשוער ומשרעת התנודה שתימדד יכול שתהיה בסדר גודל דומה למימדי היקום הידועים).
האם משתמע מכך כי כאשר עסקינן ביצורים קוונטיים כדוגמת קרינה אלקטרו מגנטית, מרחק וזמן הם בקירוב אותו הגודל עצמו בתוספת הכפלה/חילוק בקבוע מהירות האור, "C" ?
לדעתי, לפחות כפי שאנו תופסים את הזמן, התשובה לכך היא שלילית. שכידוע הזמן מאופן הגדרתו הוא גודל סקלארי המתקדם, לפחות בממוצע על פני יחידות זמן רבות, רק בכיוון אחד. בעוד מרחק (מיקום), מהיותו גודל ווקטורי, יכול שיתקדם לכיוונים שונים.
ברור שאם נתייחס לזמן כגודל ווקטורי, כמו מרבית הגדלים האחרים, בעל עוצמה וכיוון, נקבל אפשרות של "יקומים מקבילים". כך שניתן יהיה, לפחות תיאורטית, לעבור באמצעות "יקומים מקבילים" אלו אחורה וקדימה בזמן.
הצעה אפשרית לבניית מכונת זמן, המבוססת על אפקט אחר, תוצג בחלק ג' של המאמר.
פרק 5: תיאוריית המצב היציב
ברור לעין כי תיאוריה זו שהעליתי, בהכללה לשלושה ממדי המרחב הידועים, תואמת יותר, עם תנודות קלות סביב נקודת שיווי המשקל היציב, לתיאוריית מבנה היקום הידוע בשמה – "המצב היציב", ופחות לתיאורית "המפץ הגדול", הרווחת יותר. כך, כיוון והיקום נצפה כמתרחב, לפי התיאוריה שלנו, היקום במצבו העכשווי נמצא באחת משתי האפשרויות: התרחבות מכיוון פנים הכדור הדמיוני התלת ממדי הנוצר מסיכום נקודות שיווי המשקל בשלושת ממדי המרחב "כדור שיווי המשקל" בחזרה לעבר פני כדור שיווי המשקל התלת ממדית (איור 5, חץ אדום שמאלי עליון) או לחילופין מפני כדור שיווי המשקל התלת ממדי והחוצה (איור 5, חץ אדום ימני תחתון).
פה אולי המקום להוסיף שבמקרה ומסת היקום היא אכן אפסית, כפי שהנחנו, אזי משרעת האוסילציה סביב פני כדור שיווי המשקל, מצד אחד, יכולה להתרחב כמעט עד לאין סוף, ולהתכווץ כמעט עד למימדים אפסיים, מצד שני – מימדי תחילת ה"מפץ הגדול". אם כך אנו רואים שה"מפץ הגדול", לפחות בשאלת מקור תחילת היקום בנקודה סינגולרית אחת, הוא מקרה פרטי של ה"מצב היציב" כפי שתיארנו אותו.
פרק 6: חומר-חלקיק/אנטי חומר-אנטי חלקיק
כפי שהראינו עד כה, כל ריק, חלקיק, יחידת מסה או היקום הידוע עצמו נמצאים, בכל זמן נתון, בתנודה סביב פני כדור שיווי המשקל. מצבי התנודות האפשריות הן:
- "התרחבות" כפי שתוארה בפרק הקודם.
- "צמצום" מהחוץ בחזרה לעבר פני כדור שיווי המשקל (איור 5, חץ אדום ימני עליון) או מפני כדור שיווי המשקל לעבר מרכז הכדור הדמיוני התלת ממדי הנוצר מסיכום נקודות שיווי המשקל בשלושת ממדי המרחב (איור 5, חץ אדום שמאלי תחתון).
.
כך נקבל כי:
במקרה של "צמצום" (איור מס' 6) סיכום וקטור עיקום המרחב שיוצר הצמצום (בשחור במרכז) יתקזז מעט עם ווקטור עיקום המרחב שיוצרת התדירות העצמית של הנקודה (בכחול למטה), כך שסיכומם עם ווקטור עיקום המרחב שיוצרות הנקודות סביב (באדום למעלה) ייתן ווקטור עיקום פנימה (להלן: "כוח משיכה/חומר/חלקיק").

- במקרה של "התרחבות" (איור מס' 7) נקבל כי סיכום ווקטור המרחב שיוצרת ההרחבה (חץ שחור) יוסיף לווקטור עיקום המרחב שיוצרת התדירות העצמית של הנקודה (חץ כחול) כך שבסיכומם עם ווקטור עיקום המרחב שיוצרות הנקודות סביב (חץ אדום), כל עוד עסקינן במסה בסדרי גודל קוונטיים, נקבל ווקטור עיקום החוצה מפני כדור שיווי המשקל (להלן: "דחייה/אנטי חומר/אנטי חלקיק").

- במקרה של "התרחבות" (איור מס' 7) ומסה שאיננה בסדרי גודל קוונטיים, משל העובדה שווקטור עיקום המרחב שיוצרת התדירות העצמית (חץ כחול) זניח, כאמור בפרק הראשון, יכול שנקבל שווקטור עיקום המרחב שיוצרות הנקודות סביב המסה (חץ אדום) יגבר על סיכום ווקטורי עיקום המרחב שיוצרות ההרחבה (בשחור) והתדירות העצמית. משכך סיכום כל ווקטורי עיקומי המרחב יכול שייתן ווקטור עיקום מרחב פנימה, "חומר/חלקיק".
.
מכאן נדירותו היחסית של "האנטי חומר"/"אנטי חלקיק", בעיקר במקרה של התרחבות בסדרי גודל קוונטיים.
בצירוף הנחת העבודה מהפרק הראשון כי מרבית היקום מורכב מנקודות ריק כמעט מוחלט, נקבל שקרוב למחצית היקום צריך שיהיה מורכב מאנטי חומר/חלקיק – בפרק 36 דיון מורחב בחוסר היחסי של האנטי חומר ביקום.
הערה : מכאן והלאה, במאמר זה, כול שימוש במונחים "חומר"/"חלקיק" או "אנטי חומר"/"אנטי חלקיק" יהיו שימושים חלופיים.
פרק 7: מהירות האור
עד עתה, בפרק החמישי, הראנו כי בהינתן אוסילציות הרמוניות סביב "פני כדור שיווי המשקל היציב". ובהנחה סמויה שבכול הכיוונים התנאים זהים (כדור רב מימדי מושלם) מתקבלת, עם תנודות קלות סביב שיווי המשקל כאמור, תיאוריית המצב היציב. נמשיך בכיוון זה, המניח את אחידות כל הכיוונים ונישאל: האם מהירות ההתרחבות/צמצום (פרק 6) היא במהירות קבועה "C" ?
נראה שהתשובה לשאלה זו היא פשוטה ביותר: כפי שמתנהג קפיץ מתוח כשמשחררים אותו (איור 8) לתנועה הרמונית פשוטה, בהזנחת החיכוך, המהירות המקסימאלית היא בנקודה "O", מרכז הכובד של התנועה (רק אנרגיה קינטית) והנמוכה ביותר היא בקצוות, "X1" ו-"X2 " (0 – לזמן קצר מאוד).
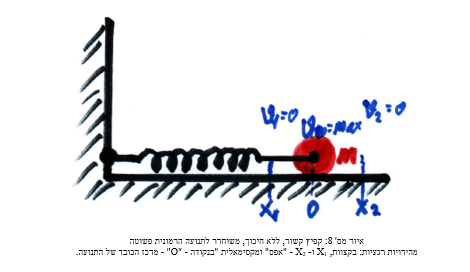
כך נוכל לתאר גם את מהירות האוסלציות סביב "פני כדור שיווי המשקל היציב" (איור 9) בכדור הרב מימדי שלנו כ- 0, בקצוות ( X1 ו- X2), לזמן קצר מאוד ומירבית, כמעט אין סופית בהנחת מימדים קוונטיים, במרכז (פני כדור שיווי המשקל – "O").

אם כך קבלנו כי מהירות האור, בהנחה שהיא המהירות האפשרית המירבית בטבע בזמן נתון, שווה למהירות הנקודתית של האוסילציה של נקודת הריק הכמעט מוחלט/היקום/החור השחור ויכולה להשתנות, על פני זמן רב, בין 0 בקצוות (X1 ו- X2 ), לכמעט אין סוף, במרכז הכובד של התנועה ("O").
- הערה: מצד אחד, מהגדרה (תורת היחסות) שמהירות האור היא המהירה האפשרית בטבע מכאן שמהירות האוסילציה איננה יכולה לעלות עליה. מצד שני, אם מהירות האוסילציה הייתה נמוכה, ואפילו לתקופה קצרה, ממהירות האור, אזי כול קרינה אלקטרומגנטית הייתה עוזבת את הייקום במיידית והייקום היה נותר מקום חשוך וקר. מכאן שנותרנו עם האפשרות היחידה – מהירויות האור והאוסילציה שוות.
נשאלת השאלה האם ממדידת השינוי במהירות האור על פני שנים רבות, נניח היום ולפני מיליארד שנה, נוכל להסיק את מצב היקום היום (מיקום מדוייק בהתרחבות הנוכחית) ובכך נוכל להסיק גם את מסת היקום, כמות החומר שבו, קבוע הכבידה העולמי "G", רמת האנרגיה האופיינית של הריק ומשתנים וקבועים רבים נוספים ?
על מדידת השינויים במהירות האור על פני זמן בהמשך, בפרק 11 ובעיקר בחלק ה' של המאמר המציע ניסוי להוכחת התאוריה.
פרק 8: תופעות נוספות
כל עוד הנחנו מבנה כדורי רב מימדי מושלם, ללא עדיפות כלשהי לציר זה או אחר, ניתן היה, את התוצאה המתמטית של תחשיב מצב היקום במימד אחד, להשליך למימדים גבוהים יותר. אם נשנה מעט את הההנחה כך שהכדור הרב מימדי לא יהיה מושלם עוד (קירבה לכזה), נקבל תנועות אוסילציות רב מימדיות משניות סביב האוסילציות המרכזיות. משל היותנו יצורים החיים בעולם של שלושה מימדי מרחב בלבד, תופעות הקורות במימדי מרחב מישניים, גבוהים יותר, או בשל אי כדוריות מושלמת, יהיו נדירות ונוכל לתאר אותם בשמות כגון: צבע, ספין …
המשך הדיון בתופעות הנוספות בפרק 26 ודוגמה בפרק 37.
פרק 9: ריבוי יקומים/"אינפלציה של יקומים"
כבר בפרק הראשון של המאמר דיברנו על נקודות ריק כמעט מוחלט מרובות. בהמשך, פרקים 2 עד 7, בנינו את האפשרות שכל נקודה כזאת יכולה להחשב יקום שלם בפני עצמו. כך ניתן להניח שהיקום המוכר לנו היום הוא נקודת ריק כמעט מוחלט, אחת מיני רבות, המרכיבה יקום גדול משלנו (נקרא לו – "יקום אב") במספר סדרי גודל שבתוכו יקומים, דמויי זה שלנו, קטנים רבים (נקרא להם – "גורי יקומים").
לדוגמה: כידוע, מרבית נפח האטום עצמו, המרחק שבין האלקטרונים לגרעין, הינו ריק כמעט מוחלט, כזה שיכולים להתמקם בו אין ספור יקומים כאלו. אם נזכור כי כול חומר, כולל הגוף שלנו, מורכב מאין ספור אטומים, נקבל שגם בתוך החומר המרכיב את היקום/הגוף שלנו סביר שקיימים אין ספור יקומים דומים, קטנים בסדרי גודל.
כול שנותר הוא להראות, את הברור מאליו, שיצור תבונתי, דמוי אדם, החיי ביקום כזה לא יכול שיבחין בגודלו היחסי של היקום (גדול או קטן בסדרי גודל), זאת בשל העובדה כי כל הגדלים, כולל גודל "דמוי האדם" עצמו, קטנים/גדלים באותו סדר גודל כך שחוקי הפיסיקה (טבע) ישארו אותם החוקים, ללא תלות בגודל. לדוגמה: ביקום גדול/קטן בשבעים סדרי גודל צריך שהמטר יהיה גדול/קטן פי 70^10 (אחד ואחריו 70 אפסים), בהתאמה, מהמטר שלנו.
פרק 10: מהירות האור וגדלים קוונטיים
נחזור לפרק הראשון של המאמר בו הזכרנו את שעולה מתורות הקוונטיים והיחסות כי: ככול שמסה קטנה יותר אורך הגל האופייני לה ארוך יותר והתופעות הקוונטיות והיחסותיות (פרק 4) משמעותיות יותר. אם כך, כאשר נחייה ביקום קטן בכ- 70 סדרי גודל מהיקום שלנו, ניתן לחשוב שהתופעות הקוונטיות בו יהיו משמעותיות יותר, דבר העומד בסתירה, לפחות לכאורה, לעקרון האינווריאנטיות של חוקי הפיסיקה, כפי שטענו בפרק הקודם, שקיימים ללא תלות בגודלו היחסי של היקום.
לשם הדוגמה לתופעות קוונטיות, נבחן את מהירות האור בשני היקומים, שכידועה גוף הנע במהירות המתקרבת למהירות האור מסתו עולה, הזמן העצמי שלו מתקצר ותופעות יחסותיות נוספות. כל זאת, בהנחה שאם במעבר מ"יקום אב" ל"גור יקום" וההפך לא נוכל להבחין בשינוי בגודלה של מהירות האור, אזי לא נוכל להבחין גם בשינוי בתופעות קוונטיות קשורות אחרות. ובכך הוכחנו, למעשה, גם אם חלקית, את עקרון האינווריאנטיות, ללא תלות בגודלו היחסי של היקום, של חוקי הפיסיקה.
כידוע, מהירות האור ביקום שלנו, נכון לנקודה העכשווית באוסילציה (פרק 7), היא בקירוב 300,000 sec/ק"מ. אם נגדיר, לשם הנוחות, את יחידות המדידה היסודיות של המרחק כמטר ושל הזמן כשניה, מהירות האור תהיה כ- 3 מיליון sec/מטר או כ- 3 מיליון (יחידות יסודיות של זמן/יחידות יסודיות של מרחק).
בפרק הקודם טענו שכל היחידות קטנות/גדלות בהתאמה, בדוגמה פי 70^10, כך שגם ב"גור היקום", הנמצא באותה נקודה באוסילציה, נוכל להגדיר את מהירות האור בדיוק באותה צורה, כ- 3 מיליון (יחידות יסודיות של זמן/יחידות יסודיות של מרחק), מתמטית (1 = 70^10 / 70^10).
כך כול צופה, בכל יקום שהוא, גדול או קטן בכל סדר גודל שהוא, ימדוד את כול הגדלים הקשורים למהירות האור בדיוק באותה עוצמה ביחס ליחידות המדידה היסודיות שיגדיר.
אם נניח, דבר שעל פניו נראה כברור מאליו, שכול יתר הגדלים הקוונטיים מתנהגים בצורה דומה, נקבל שכל צופה, בכל יקום שהוא, באותה נקודה באוסילציה, ימדוד את אותה מסה של האלקטרון ואותם קבועי פלאנק, כבידה וכיוצב"ז. דהינו: פתרנו את הסתירה, לכאורה, ועקרון האינוורנטיות של חוקי הפיסיקה, ללא תלות בגודלו היחסי של היקום, ישמר.
- הערה: כפי שעולה מתחילת הפרק, בהנחה שעוצמת התופעות הקוונטיות והיחסותיות תלויות במסה/גודל האבסולוטיים, ניתן לחשוב שככול שהיקום, בסדרי גודל, קטן יותר, התופעות בו יהיו משמעותיות יותר.
נבחן את השאלה מנקודת השקפתו של צופה מ- "יקום אב" ל– "גור יקום" (היקום בו אנו חיים, כדוגמה).
יצור תבוני, החי על "יקום אב", המביט לעבר "גור יקום", רואה את "גור היקום" ממרחק רב ובגודל ומסה של כ- 70^10 קטנים מהמצוי בסביבתו. דהינו: האפקטים הקוונטיים (כולל: אפקט המנהרה, תדירות עצמית ואורך גל אופייני) של "גור היקום", שיראה הצופה, יהיו בהתאם למסה הנמוכה מאוד (ביחס למסה המצויה בסביבתו) אותה ימדוד – למעשה בהתאם למסה היחסית שבניהם.
מתקבל, שעוצמת אפקט המנהרה, כמו גם האפקטים הקוונטיים והיחסותיים האחרים, יהיו תלויים במסה והגודל היחסיים – לא, כפי שנהוג לחשוב, באבסולוטיים – תוצאה המסתדרת, גם היא, עם תוצאת הדיון המתמטי שבפרק ועקרון האינוורנטיות של חוקי הפיסיקה.
פרק 11: הצעת ניסוי מחשבתי לבחינת התאוריה
בפרק זה, לקראת סיום חלק א' של המאמר, תחת ההנחה הקובעת שמהירות האור, המהירות המירבית בטבע, שווה למהירות האוסילציה בזמן נתון (פרק 7), נציע ניסוי מחשבתי למדידת השתנותם מאז "הולדת היקום", עד היום ולעתיד. כל זאת תחת הקביעה, התצפיתית (פרק 5), שאנחנו חיים ביקום מתרחב, כזה הכולל שתי אפשרויות לטבעו: האחת התרחבות מפני כדור שיווי המשקל והחוצה, השניה התרחבות מהפנים אל פני הכדור.
נבחן את האפשרויות:
בהתאם לאפשרות הראשונה, היקום בהתרחבות מפני כדור שיווי המשקל, שם מהירות ה- אור/אוסילציה הייתה מקסימאלית, כלפי חוץ. כך שמהירות האור שבעבר הייתה גבוהה יותר הולכת ופוחת עם הזמן. אם כך עצם שמימי שאנו מודדים היום במרחק 9 מיליארד שנות אור, ביקום כזה, הוא למעשה רחוק יותר. מתקבל שהאנרגיה האמיתית שלו גבוהה משאנו חושבים.
בהתאם לאפשרות השניה, שנראה כי היא מתאימה יותר למצבנו הנוכחי, היקום נמצא בהתרחבות מהפנים לעבר פני כדור שיווי המשקל. או אז, בהתאם לפרק 6, ובהנחה שמסתו הינה בסדר גודל קוונטי, כלפי חוץ הוא נצפה כאנטי חומר/חלקיק. כאמור, במקרה זה, מהירות ה- אור/אוסילציה שהייתה נמוכה יותר ב"הולדת היקום", שאפה לאפס, הולכת ועולה עם הזמן. כך גוף שאנו מודדים היום במרחק של 9 מיליארד שנות אור נמצא למעשה קרוב יותר משנדמה לנו. לכן האנרגיה האמיתית שלו נמוכה, בהתאם ליחס ריבועי הפרשי המרחקים, משנדמה לנו.
האם תוצאת האפשרות השניה, הקובעת שהעצמים הרחוקים ביקום קרובים בהרבה משנדמה לנו, יכול שמסבירה, ולו חלקית, את האנרגיה העצומה הנמדדת של הקוואזרים, הנמצאים בשולי היקום הידוע ?
הערה – הניסוי המחשבתי שהצגנו הראה לנו כי: באמצעות ההנחה, העולה מ"תורת הכדורים", שמהירות האור איננה קבועה בזמן (הולכת ועולה עם הזמן, כאמור באפשרות השנייה שהוצגה בתחילת הפרק) ניתן אף להסביר את האנרגיה העצומה של הקווזארים, כמות אנרגיה שאיננה מסתדרת עם חוקי הפיסיקה הקיימים. אך, למעשה, נותרנו עם הבעיה: איך להראות שמהירות האור אכן משתנה במשך תקופת זמן ארוכה כפי התחזית. לעניין זה התייחס בסוף פרק 53 שבחלק ה'.
לאחר הניסוי המחשבתי: בפרק זה, בהמשך לפרקים 5 ו- 7, קבענו כי היקום, במצבו הנוכחי, בהתרחבות מהפנים לעבר פני כדור שיווי המשקל – תקופה בה מהירות האור/אוסילציה בעליה מתמדת. נראה כי עליה זו במהירות ההתפשטות, יכולה להסביר את המושג ה"שגוי" לטעמנו, "אנרגיה אפלה", כפי ששגור בפי הדוגלים בתאוריית המפץ הגדול (בשונה מהמושגים "חומר אפל"/"אנרגיה אפלה" בפרק 2).
לטעמנו שגוי מהטעם ש"אנרגיה" – לכאורה זו, נובעת מהמצב הקוונטי של אוסילציית היקום בהתפשטות הנוכחית. ללא קשר לאנרגיה אפלה, כלשהי.
התייחסות למקור/חוק שימור האנרגיה, בעניין זה, בהמשך בחלק הרביעי ובעיקר בפרק 46 של המאמר.
פרק 12: היווצרות הקוונטים
עד כה, בפרקים הקודמים, דיברנו על מדידות של מרחקים, מהירויות, מיקומים וכד'. הנחה סמויה, לצורך מדידות אלו, הייתה כי: ניתן להגדיר מרחב הכולל – שלושה, ארבעה או יותר מימדים.
כך, אם נאלץ הגדרת מימדים על מרחב, שבהנחה הינו חסר מימדים בטבעו, נקבל כי הגדרת המימדים כשלעצמה יצרה אפשרויות, שלא היו קיימות קודם, למדידות והגדרות של: מיקום, מהירויות, מסה, נקודות ריק כמעט מוחלט, שעמדו בבסיסו של מאמר זה, ושל אורך גל, תדירות עצמית וכיוצ"ב.
כמקובל היום, מסורתית, המרחב מוגדר בשלושה מימדי מיקום (לדוגמה: x, y, z) ולאחרונה מימד רביעי לזמן. הגדרת המימדים, למעשה, היא זו שיוצרת מגבלות כאלו ואחרות (ראה גם סוף פרק 3). לדוגמה: מהגבלת המימדים שייצרנו, על המרחב חסר המימדים, נובע כי מדידת חלקיק קוונטי בסיסי בזמן מדוייק, למעשה, עוצרת את רצף הזמן, כך שבנקודת הזמן הבאה (המדידה הבאה) נוכל למצא את אותו החלקיק הקוונטי בכל מקום אחר על פונקצית הגל שלו עצמו. שני מיקומים שלא חייבים להתישר עם העיקרון, העולה מתורת היחסות, הקובע שמהירות האור היא המהירות המרבית – התקבל עיקרון אי וודאות במיקום. באותה צורה ניתן להראות שמדידת חלקיק קוונטי במיקום מדוייק גם היא עוצרת את רצף הזמן כך שהאילוץ למצא את החלקיק באותו מיקום בדיוק, במדידה הבאה, נותן את עיקרון אי הוודאות בזמן. דהינו: מגבלת המימדים, על יקום חסר המימדים, היא זו שיוצרת את עקרונות אי הוודאות, בזמן ובמיקום, אשר הינם מהעקרונות היסוד של תורת הקוונטיים – למעשה יוצרת את תורת הקוונטים עצמה.
נשאלת השאלה – האם ניתן היה להגדיר את המרחב בצורה אחרת משעד היום הוגדרה, לדוגמה: כווקטור הכולל שלושה מימדי זמן ומימד מיקום אחד (ראה גם פרק 44) ?
לטעמי, רק מההבנה שהגדרת המרחב כמקובל היום היא הגדרה שרירותית, אחת האפשרות מיני רבות, ניתן להסיק שקיימות אפשרויות רבות נוספות ושונות להגדרת סט מימדים עבור מרחב נטול מימדים שכול אחת יוצרת הבנה ותפיסה שונה של היקום, למעשה "יקום שונה", הדומה למושג "יקומים מקבלים", כפי שהוזכר בסוף הפרק הרביעי. במקרה זה, כיוון וכל הגדרה שונה של המרחב הבסיסי, נטול המימדים, תיתן הבנה שונה, הכוללת חוקי טבע (פיסיקה ומתמטיקה אחרים), וחלקית של היקום כולו, לא נחפש קוהרנטיות מושלמת בין היקומים השונים הנוצרים מעצם ההגדרות השונות, אך בהחלט שנחפש חוקי טבע כוללניים שיתאימו לכל סט מימדים אפשרי.
פרק 13: סיכום לחלק א'
בפרק הראשון, העלינו לדיון את עיקר החידוש שבמאמר והראנו כי התורה הקוונטית לא רק שאיננה סותרת לתורת היחסות ולכוח הכבידה הנובע מימנה, כפי שנהוג לחשוב, אלא אף, בשילוב הגדרת המושג נקודות ריק כמעט מוחלט, חוזה את עיקום המרחב ובכך, בדרך דומה העולה מתורת היחסות הכללית, מנבאת את קיומו של כוח המשיכה.
בהמשך, הראנו כי, בשילוב תורות "הכדורים" והקוונטים, ניתן להסביר תופעות נוספות, כדוגמת: חומר/אנרגיה אפלים בפרק השני, חומר/אנטי חומר בפרק השישי וכנראה תופעות רבות נוספות.
לבסוף, בפרק האחד עשר, הצענו ניסוי מחשבתי למדידת השתנות מהירות האור, עם הזמן. ניסוי שתוצאותיו יכולים, אולי, להסביר תופעות נוספות, כדוגמת האנרגיה הגבוהה הבלתי מוסברת של הקוואזרים.
בסה"כ, בחלק זה של המאמר, עסקנו, בעיקר, בתופעות הקוונטיות של מבנה היקום. אך כפי שעלה כאן, קיימות אין ספור/סוף נקודות ריק כמעט מוחלט כאלו (פרק 1) שכול אחת, כלפי חוץ, מתנהגת כחומר/אנטי חומר, חלקיק/אנטי חלקיק (פרק 6). כך מנקודת מבת חלקיקית נקבל תופעות נוספות, קלאסיות, כפי שמרביתם מוכרות.
ונסיים את חלק זה, חלק א' של המאמר, בשאלה העולה מהפרק הקודם – 12.
האם קיימת אפשרות שבעתיד יוגדרו חוקי מתמטיקה (פיסיקה) כוללניים, נטולי מימדים ?
.
חלק ב': הדואליות של ראשית הצירים
פרק 14: הקדמה לחלק ב'
חלק א' של המאמר התרכז בדיון בגופים: מסות ונקודות ריק כמעט מוחלט, הנטועים על מקומם, ללא תנועה במרחב. כך, רק מין-המתבקש הוא, כי הדיון בחלק זה ימשיך ויתעמק בהשפעת התאוריה שפותחה גם במקרה של גופים בתנועה, דהינו: המשך הדיון הראשוני, מהחלק הקודם בתנועת אוסילציות סביב מרכז הכובד, כמו גם דיון בתנועה של מרכז הכובד עצמו – אם במהירויות ובכיוונים קבועים, או בשינויים שלהם ("להלן: "תאוצה").
כפי שנראה בהמשך, תנועה של מרכז הכובד של נקודות ריק כמעט מוחלט (פרקים 28 ו- 29), מועילות בהסבר תופעות שלעת עתה המדע יתקשה להציע להן הסבר טוב יותר.
פרק 15: כדור הארץ כמרכז היקום
ניראה שכול ילד קטן יכול להבין כי: כיוון והאור נראה כמתקרב/מתרחק במהירות האור, הוא זה הנע במהירות קבועה "C", מהירות, שבהתאם להנחת היסוד של תורת היחסות הפרטית, גם המהירות המקסימאלית האפשרית בטבע.
בעבר האמנו שכדור הארץ עומד במרכז, והשמיים, הרקיע סובבים סביבו. משהתבררה הטעות, שמנו את מערכת השמש במרכז הגלאקסיה שלנו (שביל החלב), כשהגלקסיה מוקמה כמרכז היקום. בשלב מאוחר יותר התברר שאנחנו, הארץ, מערכת השמש או הגלאקסיה, כלל לא מהווים מרכז כלשהו ושלמעשה כדור הארץ הוא חלק ממערכת שמש, אחת מיני מערכות דומות רבות בתוך גלאקסיות רבות דומות, וללא יחוד כלשהו למרכזיות.
ניראה שמרכזיות זו והחשיבות היתרה שאנו מיחסים לעצמנו עדיין לא שככה. אנו ממשיכים, ללא סיבה נראית לעין, לשים את עצמנו כמרכז היקום – בראשית הצירים של מערכת הצירים "הסמויה" שהונחה בדיון בחלק הראשון של המאמר הקובעת, גם אם לא במתכוון, בהתאם למקובל, את מרכז הכובד של המסות כראשית הצירים (להלן: "מערכת הצירים הישנה", "מערכת הצירים הקיימת" או "מערכת הצירים הסמויה"), ומאמינים שקיים תאום, נסתר כלשהו, בין כל סוגי הקרינה האלקטרומגנטיות הרבים הידועים, כך שכולם, בכל מקום במרחב, יודעים האחד על השני והחליטו באמצעות תקשורת כזאת או אחרת ביניהם לנוע, סביבנו כמרכז, בתיאום, בקירוב באותה מהירות, לא פחות ולא יותר מ – "C". מהירות שאף, כנטען בחלק הראשון, משתנה עם הזמן, בין – 0 לכמעט אין סוף.
פרק 16: מי-הו הנע ומי-הו הנח ?
מכאן עולה השאלה הבאה: האם, לצורך תיאור המציאות, קיימת אפשרות נוספת לקביעת מערכת צירים ?
לטעמי, כאמור בפרק הקודם, יהיה זה בלתי סביר לחשוב שכול נקודות הריק הכמעט מוחלט המרכיבות את המרחב (ראה איור מס' 2 בחלק א') המתוארות, כל אחת, כבעלות תדירויות ואורכי גל עצמיים אופייניים (גם קרינה אלקטרומגנטית) ינועו כולן יחד ובתאום באותה מהירות "C". סביר יותר יהיה להניח שהן, כולן, אינן נעות כלל, מהירות "0". בעוד הגופים בעלי המסה, כולל אנו הצופים, הם אלו המסוגלים לתנועה במרחב שבניהם.
כזכור, בהתאם לפרק הראשון בחלק הראשון של המאמר, הקובע, בין היתר, כי אורך הגל האופייני לנקודת ריק כמעט מוחלט במימדים קוונטיים שואף לאין סוף, התקבל, שם, כי חלקיק חסר מסה או בעל מסה זניחה, למעשה הינו סוג של גל – קרינה אלקטרומגנטית, אם באורכי גל של האור הניראה או של קרני: x, γ, β, α וכיוצ"ב.
לכן, משנניח, בחלק זה, בניגוד לחלק הראשון, שנקודות הריק הכמעט מוחלט המרכיבות את המרחב אינן גל, הן נטועות על מקומן ללא תנועה או תדירות עצמית (או לפחות כך לגבי מרכז הכובד שלהן – הרחבה בהמשך, פרק 30), מתקבלת תמונת ראי: מתקבל כי מהירות האור/הקרינה האלקטרומגנטית היא זהותית – "0", ודווקא מסות, כתלות בגודל, יהיו בעלי אורך גל ותדירות עצמית אופייניים – כך שמסות גדולות מאוד ינועו בתנועה הרמונית במהירות קבועה – "C", לכול הכיוונים, בעת ובעונה אחת. מהירות שראוי, משל האור כלל איננו נע בה, שתיקרא "מהירות המסה", "מהירות האוסילציה" או ה"מהירות המקסימלית".

מכאן (ראה איור מס' 10) שמנקודת מבטו של צופה הממוקם על המסה, כדור הארץ לצורך העניין, האור יראה כנע במהירות האור – "C". בעוד מקור האור, בעל המסה שנע בהשפעת כוח הכבידה איתו בצמידות, יצפה כעומד במקום.
פרק 17 : מערכת הצירים
מהידועות היא שקביעת מערכת הצירים היא עניין שרירותי שאיננו צריך שישפיע על חוקי הפיסיקה ושבמרבית המקרים קביעת ראשית הצירים בנקודה נחה מקל על החישובים, המתמטיים ופיסקליים כאחד. אם כך, רק מן המתבקש הוא שבחלק זה של המאמר, בניגוד לחלק הראשון (ראה פרק 15), נקבע את ראשית הצירים, שרירותית על אחת מנקודות הריק הכמעט מוחלט שבאיור 2 בחלק הראשון (ראה איור מס' 11 למטה) – (להלן: "מערכת הצירים החדשה").
כך כל נקודות הריק הכמעט מוחלט, למעשה, לא ינועו (מהירות – 0): אחת ביחס לרעותה וביחס לראשית הצירים שנקבעה.

פרק 18: טרנספורמציית לורנץ
נבדוק את השלכות ההנחה כי מהירות האור, נקודות הריק הכמעט מוחלט, זהה או קרובה מאוד ל – "0" על חיבור מהירויות, טרנספורמציית לורנץ.

נתייחס לשני מקורות אור (חלליות) שנראות לצופה נח כנעות כל אחת במהירות האור בכיוונים מנוגדים (ראה איור מס' 12), כיוון שבמערכת הצירים החדשה הנחנו שמהירות האור, ביחס לראשית הצירים, היא "0", אזי המהירות היחסית בין מקורות האור (החלליות), תהיה – "0" = "0" + "0". מכאן שחיבור המהירויות של שתי חלליות, הנעות, ביחס לראשית הצירים החדשה, כאמור, כל אחת לכיוונים מנוגדים במהירות הקרובה ל – "0", נותן מהירות יחסית הקרובה ל – "0" – אותה המהירות שקבענו לאור עצמו, "C" במערכת הצירים הישנה.
בנוסף, נסתכל על ההכללה לטרנספורמציית לורנץ, מהפרק הראשון בחלק הראשון, וניווכח כי חיבור מספר סופי, גם אם גדול מאוד, של אפסים – מהירות כל אחת מהרכבות האחת על גבי השנייה ביחס לראשית הצירים החדשה – עדיין, במערכת הצירים החדשה, ייתן את המהירות שלנו יחסית לכדור הארץ כקרובה ל – "0" – היא מהירות האור ביחס לראשית הצירים החדשה, כפי שהנחנו, השווה ל – "C", במערכת הצירים הישנה, כאמור.
דהינו: כפי שעולה מתורת היחסות הפרטית, חיבור מספר סופי, גם עם גדול מאוד, של מהירויות עצמים, הנראים לצופה כנעים כל אחד במהירות הקרובה למהירות האור "C", לעולם יתן "0" במערכת הצירים החדשה, ובמערכת הצירים הישנה לא יעבור את מהירות האור עצמה.
פרק 19: מהירות המסה כלפי המרחב
כיוון שמהמוסכמות היא שהגדרת מערכת הצירים אין בה מלשנות את חוקי הפיסיקה, כפי שנטען כאן כבר בפרק 17, והיות ובמערכת הצירים החדשה שהגדרנו, בניגוד לקודמת, כל נקודות הריק הכמעט מוחלט עומדות ללא תנועה ביחס לראשית הצירים; אזי התדירות העצמית ואורך הגל, כפי שהיו אופייניים במערכת הצירים הישנה, הסמויה (כזכור מפרק מס' 15, נבעה מההשקפה שאנחנו המרכז והאור נע סביבנו), בגדלים קוונטיים, יתקבלו, במערכת הצירים החדשה, כתמונת ראי, למסות גדולות. דהינו: התדירות העצמית ואורך הגל – כתמונת ראי לחלק הראשון, כאמור – יהפכו להיות משמעותיים יותר דווקא ככול שהמסה גדלה. כך שלושת הנקודות האופייניות לתורת הקוונטים, כפי שהוזכרו בפרק הראשון של החלק הראשון, במערכת הצירים שלנו, הקובעת את ראשית הצירים כנקודה נחה כאמור, תשתנינה כדלקמן:
- למסה, גם כזו השואפת ל – ∞ , מוצמדים תדירות עצמית ואורך גל אופייניים.
- ככול שהמסה גדולה יותר (להלן: "מימדי מסה קוונטיים") אורך הגל האופייני ארוך יותר.
- ככול שהמסה קטנה יותר אורך הגל האופייני קצר יותר, עד שהופך להיות חסר משמעות בגדלים שאינם מסה קוונטיים.
.
כך, למעשה, במערכת הצירים החדשה, ככול שהמסה גדולה יותר אורך הגל האופייני לה ארוך יותר. וניתן, כשהמסה שואפת לאין סוף, לתאר אותה כנעה באוסילציה הרמונית, לכל הכיוונים, במהירות קבועה רגעית מקסימאלית – "C"; מהירות אוסילציה מקסימאלית ההולכת ופוחתת ככול שהמסה קטנה יותר עד למהירות – "0" כאשר עסקינן בנקודת ריק כמעט מוחלט – מסה שואפת ל- "0".
נסתכל על איור מספר 13: בו צופים מס' Ⅰ ו- Ⅱ, כדוגמה לכול צופה אחר בעל מסה גבוהה, בהשפעת כוח המשיכה הפועל ביניהם, במערכת הצירים החדשה שהגדרנו, ינועו בצמידות באוסילציה הרמונית לכול אחד מהכיוונים, בעת ובעונה אחת, במהירות הקרובה ל – "C". מכאן שהם יראו את כל אחד ממקורות האור, A עד E, כמתקרב/מתרחק אליהם/מעברם בדיוק באותה המהירות שלהם – הקרובה ל – "C", כאמור.

פרק 20: המושגים תנע וחוק שימור התנע
כששני גופים (לצורך הנוחות נניח כדוריים) מתנגשים, ונניח שהכוחות המופעלים במהלך ההתנגשות הם כוחות משמרים בלבד (ללא חיכוך, פלסטיות וכיוצ"ב) נקבל, גם במבט אינטואיטיבי, כי הגופים יירתעו האחד מהשני, כך שמבחינה כמותית התנע של המערכת טרם ההתנגשות (סכום המסות כפול המהירויות שלהם) לפני ואחרי יהיו שווים.
אך מה לגבי גוף שפולט חומר (מאבד מסה) ?
כידוע, גם כאן, בצורה פחות אינטואיטיבית, בהתקיימות חוק שימור התנע, הגוף שאיבד מסה (מטוס סילון לדוגמה) יגביר את מהירותו לכיוון הנגדי.
בהתאם לפרק מס' 16 והפרק הקודם 19, ב"מערכת הצירים החדשה", ככול שהמסה קטנה יותר, אורך הגל האופייני קצר יותר ומהירות האוסילציה הולכת ופוחתת, דהיינו: קיבלנו שבאיבוד מסה מהירות הגוף, במערכת הצירים החדשה תרד.
מכאן שמנקודת מבטנו, כיוון שנותרנו באותה המהירות בדיוק, והיות ומה שאנחנו רואים זה את המהירות היחסית שביננו, נחווה את התמונה ההפוכה – מבחינתנו מהירות הגוף (המטוס) שאיבד מסה, תעלה.
הערה: הדיון הנ"ל, כמובן, נכון גם לגוף שמוסיף מסה (נדבקת, מצטרפת אליו מסה נוספת), בשל תוספת המסה, מהירותו במערכת הצירים החדשה תעלה, לכן המהירות היחסית שבינינו, אותה אנחנו חווים, תפחת.
אם כך ראינו שמנקודת השקפה של מערכת הצירים החדשה ניתן לקבל הסבר אינטואיטיבי, לפחות איכותי, לחוק שימור התנע, כדוגמה.
פרק 21: השתנות מהירות האור
כאמור בפרק 7 של חלק א', אנו חיים על נקודת ריק כמעט מוחלט (ייקום, חור שחור) אחת מיני רבות, בעלת מסה, תדירות עצמית ומהירות אוסילציה המשתנה, עם הזמן, בין "0" בקצוות למירבית, כמעט אין סופית, במרכז (פני כדור שיווי המשקל). בהתאם לפרק 19 ואיור מס' 13 שלו, אנו – הצופים, נראה את כל מקורות האור כמתקרבים/מתרחקים אלינו/מאיתנו באותה מהירות "C", שכאמור שווה למהירות האוסילציה הרגעית שלנו ומשתנה בין "0" לכמעט אין סוף. נוסיף כאן כי: מהירות האוסילציה הרגעית, המירבית, האבסולוטית במרכז (פני כדור שיווי המשקל) הינה ביחס ישר (במערכת הצירים החדשה) למסת נקודת הריק הכמעט מוחלט.
פועל יוצא של השתנות מהירות האוסילציה הוא: שמהירות האור, המהירות הנצפית של כול נקודות הריק הכמעט מוחלט בעלות המימדים הקוונטיים ושל כול סוגי הקרינה האלקטרומגנטית, המרכיבים יחד את המרחב, תהיה, ללא צורך בתאום נסתר כלשהו (ראה פרק 15), זהה סימולטנית למהירות האפשרית הרגעית המירבית בטבע – היא מהירות האוסילציה – ותשתנה עם הזמן, בין "0" לכמעט אין סוף.
פרק 22: תבנית התאבכות דרך שני סדקים – ניסוי (יאנג)
בהתאם לניסוי, כשנעביר אור ממקור אור רחוק (קרינת לייזר/מונוכרומטית) דרך שני סדקים תתקבל תמונת התאבכות, כאילו שגל האור עבר בו זמנית דרך שני הסדקים – תופעה גלית אופיינית. גם כאשר נעביר, פוטון אור בודד, דרך שני הסדקים תתקבל אותה תמונת התאבכות כאילו שהפוטון היחיד עבר דרך שני הסדקים בעת ובעונה אחת (עיקרון אי הוודאות).
אך בדרך תמוהה, כאשר נמדוד את האור או הפוטון הבודד, בשימוש בשני גלאים הממוקמים על כל אחד מהסדקים או גלאי אחד בלבד הממוקם על אחד מהם, כעובר רק דרך אחד הסדקים (ולא דרך השני), תמונת ההתאבכות תעלם ולא תופיע עוד. התמונה שתתקבל תהיה תמונה האופיינית לחלקיק/ים שעבר/ו דרך סדק אחד בלבד – (להלן: "קריסת פונקציית הגל").
- הערת ביניים: כאן, אולי, המקום להציע ניסוי לבדיקת הגבול הקוונטי. נציע להשתמש ברשת חורים/סדקים (נניח 100 = 10 xס10, דקים), הכוללת גלאים הממוקמים על מספר משתנה של נקבים. ואז לבדוק את קיומה/אי קיומה של תמונת ההתאבכות ועוצמת השיאים המתקבלים על המסך. הכול כתלות במספר: הנקבים הפתוחים והגלאים.
.
כזכור, בחלק זה, משקבענו את ראשית הצירים על מקור האור, קיבלנו שהאור, ביחס לראשית הצירים, הוא הקבוע במקומו ולנו הצופים מוצמדים תדירות עצמית ואורך גל אופייניים המתוארים כתנועה באותה המהירות, בעת ובעונה אחת, ולכול הכיוונים.
מכאן, בשל היותנו גל, ככול שנמדוד/נסתכל על האור, הקבוע במקומו בראשית הצירים, דרך שני הסדקים יחדיו, הראיה שלנו תתנהג כגל וניראה, בעת ובעונה אחת, דרך שני הסדקים – מתקבלת תמונת התאבכות.
אך משנבצע מדידה, למעשה באופן רגעי, זנחנו את התצפית הגלית, הסימולטנית משני הסדקים בעת ובעונה אחת (אילוץ מדידה דרך סדק 1). לכן ברור שמנקודת מבט של החלק הראשון, כאילו האור הוא זה שנע, תתקבל תמונה אופיינית לסדק אחד פתוח והשני חסום (רגעית איננו מודדים דרכו); האור יראה כעובר דרך סדק אחד בלבד ולא תופיע עוד תמונת ההתאבכות האופיינית לגלים. כמובן שבכול מדידה נוספת, בלתי תלויה, נצפה, ריגעית וללא יכולת ניבוי (אלה אם אנחנו מכירים בצורה מדויקת את פונקציית הגל העצמית שלנו עד כדי ביצוע חישובים מדויקים עליה), דרך סדק אחד בלבד. לכן, מנקודת מבט של החלק הראשון, נקבל שהפוטון או הגל עברו באופן מיקרי (עיקרון אי הוודאות) רק דרך אחד מהסדקים – "קריסת פונקציית הגל". שאלה מעניינת תהיה: מה יקרה, האם ומתי תקרוס פונקציית הגל, כשנשתמש ביותר משני סדקים עם מספר משתנה של גלאים (ראה הערת ביניים בתחילת הפרק).
מתקבל שעיקרון אי הוודאות בניסוי יאנג הוא תוצאה ישירה מהגדרת ראשית הצירים על האור, העומד ללא תנועה ביחס לראשית הצירים החדשה כאמור, ואילוצי המדידה, המבטלות, גם אם באופן רגעי, את התדירות העצמית שלנו עצמנו וכפועל יוצא גם את תבנית ההתאבכות האופיינית לגלים.
בצורה דומה ניתן להראות שעיקרון אי הוודאות כולו נובע מהיותנו, הצופים, פונקציית גל. מרגע שנבצע מדידה למעשה, רגעית, ביטלנו את פונקציית הגל העצמית שלנו ומצאנו את עצמנו בנקודה אפשרית אחת על פונקציית הגל העצמית. מכאן שבמערכת הצירים הקודמת נצפה את האור או הגל במיקום אפשרי אחד על פונקציית הגל שלו. בכול מדידה נוספת, שאינה קשורה כמובן, המבטלת, גם היא, את פונקציית הגל העצמית שלנו, כאמור, נקבל את הגל הנצפה בכל מקום אפשרי אחר. מיקום אשר, במערכת הצירים הישנה, איננו חייב לתאום את המהירות המירבית בטבע, אך כן חייב לתאום לעובדה שאנחנו הצופים לא עברנו את המהירות המירבית בטבע (מהירות האור הריגעית) – למעשה התנועענו כגל, באחידות, במהירות האור הריגעית, לכול הכיוונים.
פרק 23: שקילות נקודת ההשקפה
כבר בפרק 17 טענו שחוקי הפיסיקה אינם תלויים בקביעה השרירותית של ראשית הצירים. משכך ברור ששתי האפשרויות, שהצגנו, לקביעת ראשית הצירים: אנחנו כמרכז מערכת הצירים, כמקובל, או מרכז מערכת הצירים על נקודות הריק הכמעט מוחלט (אור), בכלל ובפרט במקרה של נקודות ריק כמעט מוחלט במסה גבוה – תהינה שקולות. מכאן שחוקי הפיסיקה, עבור נקודות ריק כמעט מוחלט כאלו, פרט להתאמות המתבקשות (פרק 19), ישארו כפי שהם, ללא תלות במערכת הצירים שהוגדרה. בעוד שעדיין, בד"כ, מרבית התופעות הפיסיקאליות, בעיקר לטווח הקצר בו השינויים במהירות האור ניתנים להזנחה, יהיו נוחות יותר לתיאור במערכת צירים הישנה, הסמויה וחלק אחר בחדשה.
במקרה של תצפית בנקודות ריק כמעט מוחלט במסות אפסיות (לדוגמה: פוטוני קרינה אלקטרומגנטית), כמו שהסקנו בפרק הקודם העוסק בניסוי יאנג, בשל היותנו גל, עם כול ביצוע תצפית, יקשה עלינו להסתכל על נקודות הריק מנקודת מבט של מערכת הצירים הישנה. לכן במקרה כזה נאלץ להסתפק, בעיקר, בהסתכלות מנקודת מבט של מערכת הצירים החדשה; לפיה (פרק 17) כול נקודות הריק הכמעט מוחלט נעות במהירות "0", האחת ביחס לראותה וביחס לראשית הצירים.
פרק 24: הגדרת המושג מסה מנקודת מבט קוונטית
עד עתה התייחסנו למסה כמושג קלאסי, כמעט ללא קשר לקוונטיים, ברור מאליו. נראה שהגיע הזמן לעצור לרגע ולהביט על המושג מנקודת השקפה הקוונטית.
הטענה: "מסה היא עיקום המרחב, נטו, אשר חווה אוסף המצבים הרגעיים של כול פונקציות הגל של נקודות הריק הכמעט מוחלט המרכיבות מרחב מוגדר (סופרפוזיציה), בנקודת זמן".
כבר בפרק הראשון של המאמר (חלק א'), במערכת הצירים הישנה שאנחנו במרכזה, ראינו שאורך הגל האופייני לנקודת ריק כמעט מוחלט הוא גדול מאוד, למעשה, שואף לאין סוף. ובפרק 22 נוכחנו בקיומו של עקרון אי הוודאות, ממנו נובע, בין היתר, כי: בזמן נתון נוכל למצוא את נקודת הריק הכמעט מוחלט בכל מקום אפשרי על פונקציית הגל שלה עצמה ולהתנהג, כלפי חוץ, כחומר או אנטי חומר (פרק 6).
כיוון ומספר המצבים האפשריים של פונקציות הגל העצמיות, בנקודת זמן נתונה, הוא כמעט אין סופי, נקבל שככול שגדול יותר מספר נקודות הריק הכמעט מוחלט, מאותו סדר גודל (על סדר הגודל בפרק 9 שבחלק א' ובפרק הבא), המרכיבות את המרחב המוגדר, פונקציות גל עצמיות של נקודות ריק כמעט מוחלט רבות יותר מתקזזות, בהתאבכות הורסת, עם פונקציות הגל של האחרות. נטו, נותרנו עם סכום פונקציות הגל העצמיות שאינן מתקזזות – סכום שכאמור הולך וקטן עם העלייה במספר נקודות הריק הכמעט מוחלט, מאותו סדר גודל, המרכיבות את המרחב.
מכאן שפונקציית הגל הכוללת, נטו, של המרחב המוגדר, בכל נקודת זמן, קטנה עם העלייה במספר ובצפיפות נקודות הריק הכמעט מוחלט (יחס הפוך) מאותו סדר גודל, הכלולות בו. למעשה נקבל (ראה פרק 1) כי: עם הקיטון בפונקציית הגל, נטו, של המרחב המוגדר, סה"כ סיכום ווקטורי עיקום המרחב החיצוני שיוצרות כול הנקודות סביב למרחב המוגדר (ראה איור מס' 3, בהתאמות המתבקשות – חצים אדומים), הנשאר, על המרחב המוגדר, כשהיה, הולך וגובר על עיקום המרחב ההולך ו"קטן" (חצים כחולים) שיוצר המרחב המוגדר מנגד – כך שסה"כ סיכום ווקטורי עיקום המרחב, נטו, מכל הכיוונים ובכל המימדים האפשריים, הוא חיובי, יותר ויותר, לתוך המרחב המוגדר והמרחב המוגדר מאין "מוחזק" ע"י המרחב החיצוני ב"שיווי משקל יציב", הולך ומתחזק, בדומה להגדרה הקלאסית למסה "התנגדות של גוף לשינוי מצבו".
מכאן, וכפי שטענו בתחילת הפרק, המסה איננה עוד קבוע יסודי של החומר. אלה שהיא, מעבר לתלות במהירות/תאוצה, לפי תורת היחסות הכללית, תלויה בתמונת ההתאבכות המלאה (בונה + הורסת) של פונקציות הגל של כול נקודות הריק הכמעט מוחלט המרכיבות את החומר, אשר משפיעה על עיקום המרחב, נטו, שיוצר המרחב המוגדר. בפרק הבא נדון בשינויי המסה כתלות בצפיפות.
פרק 25: המסה כתלות בצפיפות
בפרק הקודם ראינו, בהנחה שמספר נקודות הריק הכמעט מוחלט איננו משתנה, כי התנגדות המרחב החיצוני לשינוי במצבו של מרחב מוגדר הולכת ומתחזקת עם העליה בצפיפות, מכאן שמסת המרחב המוגדר עולה, גם היא, עם העליה בצפיפות. והכול כשמדובר בצפיפות מאותו סדר גודל (לא יקום אב או גור יקום של נקודת ריק כמעט מוחלט שכיכה במרחב המוגדר – ראה פרק 9).
מכאן שככול שנקטין את ניפחו של המרחב המוגדר, נקבל כי מסתו תלך ותעלה עד לנקודה (מעבר פאזה) בה המרחקים בין נקודות הריק הכמעט מוחלט המרכיבות את המרחב המוגדר יהפכו לקטנים יותר מאורך הגל של התדירות העצמית השכיכה של נקודות הריק הכמעט מוחלט המרכיבות אותו. אז פונקציות הגל יתקשו יותר ויותר לבטל האחת את השניה בהתאבכות הורסת ונקבל קיטון פתאומי במסה. מעבר פאזה שכזה צפוי שיקרה – במחזוריות – כול סדר גודל של כ- 70^10 (ראה פרק 9), אנלוגי לקיטון נפח בסדר גודל של כ- 140^10.

נראה כי לתופעה שתיארנו עדויות טבעיות. כידוע קריסת כוכב מאסיבי לחור שחור היא תהליך מחזורי (מספר מעברי פאזה) של קריסה, זריקת חומר, וחוזר חלילה מספר פעמים, עד לקריסה הסופית.
פרק 26: הכדור הרב מימדי
טרם נעבור לדון בתנועה של מרכז המסה, נחזור לכדור הרב מימדי/נקודת הריק הכמעט מוחלט, במערכת הצירים הישנה, שאנחנו במרכזה, הנעה בתנועה הרמונית פשוטה (פרק 7) סביב מרכז הכובד של התנועה, פני כדור שיווי המשקל (איור 9), כאשר (ראה פרק 1) השפעת המרחב על נקודת הריק הכמעט מוחלט מתקזזת עם השפעת הנקודה מנגד, כך שניתן לראות את הכדור הרב מימדי כמוחזק (מחובר למרחב), במרכזו הדמיוני, בשיווי משקל רופף.
בשונה מהקואורדינטות, (x, y, z) שהשתמשנו בהן בפרק 12, נסתכל על האוסילציה התלת מימדית, הפעם תוך שימוש בקואורדינאטות כדוריות (r, ϕ ,θ). מתקבל שעיקר תנועת האוסילציות היא פנימה והחוצה, בכיוון הרדיוס "r".
כך כול רכיב תנועה בכיוון אחר, אחת הזוויות לדוגמה, אם בשלושה מימדים או יותר, יכול שתגרום לחוסר איזון זמני (אוסילציות הרמוניות משניות) של הכדור ביחס למרכז המסה, לתנועה קטנה של מרכז המסה במרחב ובכך יתכנו תופעות נוספות (כאמור בפרק 8) ואף יכול שיוסברו קיומם של סוגי חלקיקים נוספים לידועים היום. בנוסף, כאמור בפרק 8, ככול שהאוסילציות המשניות יהיו במימדים גבוהים יותר (מעבר למרחב הכולל שלושה מימדים למרחב ואחד לזמן), התופעות שיגרמו יהיו נדירות יותר ולזמני חיים קצרים יותר.
דוגמה לתופעה הנגרמת כתוצאה מהאוסילציה פנימה והחוצה, סביב הרדיוס "r", בפרק 37.
לצורך המעבר לפרק הבא, העוסק בתנועה של מרכז המסה, נזכיר כי: ככול שעולה מסת הגוף קטן ווקטור עיקום המרחב שיוצרת המסה נגד עיקום המרחב החיצוני (ראה פרק 1), מכאן שמתגבר עיקום המרחב נטו לתוך הגוף וניתן לראות את הכדור כקשור למרחב, במרכזו, חזק יותר.
פרק 27: תנועה של מרכז המסה
כאמור בסוף הפרק הקודם, ככול שעולה מסת הגוף ניתן לראות את מרכז הכובד של הכדור כקשור חזק יותר ויותר למרחב. מכאן, שלצורך שינוי מהירות מרכז המסה של הכדור או כיוונה (הקניית תאוצה), שיש להשקיע עבודה/אנרגיה הולכת וגוברת עם העלייה במסה.
בסופו של תהליך, כאשר מהירות מרכז הכובד של הגוף תתקרב למהירות האוסילציה העצמית = מהירות האור הרגעית שלו, נקבל: בהתאם לתורת היחסות הקובעת כי עליה במהירות גוררת גם עליה במסה, שסיכום ווקטור עיקום המרחב פנימה (איור 3, חצים אדומים), הנשאר כשהיה, עם ווקטור עיקום המרחב ה"מוקטן" (עד כדי גודל חסר משמעות – "0" במסה גבוהה, גם כזו הנגרמת בשל העלייה במהירות, שאיננה מסדר גודל קוונטי – ראה ההתייחסות לתורת הקוונטים נקודה שלישית בפרק הראשון) שיוצרת המסה הגדלה מנגד (איור 3, חצים כחולים) יהיה, נטו, שווה לווקטור עיקום המרחב פנימה. ווקטור שגודלו, במקרה של מרחב ריק כמעט מוחלט, למעשה, כמעט אין סופי ושווה (לפי ההכללה לטרנספורמציית לורנץ שהוצעה בפרק 1), לכל היותר, לעוצמת עיקום המרחב שיוצרת נקודה אחת, בעלת מסה אפסית.
מכאן שמסת הגוף תהפוך להיות כמעט אין סופית והאנרגיה שתידרש (E = M x C^2), לצורך הגברה נוספת של המהירות, האטה או שינוי כיוון, תהיה גדולה יותר ויותר, עד שגם היא תהיה כמעט אין סופית. כך שנראה שלעולם מהירות מרכז הכובד של הגוף לא תוכל להגיע למהירות האוסילציה היא מהירות האור הרגעית.
פרק 28: תנועת נקודת ריק כמעט מוחלט במרחב (פוטונים)
כבר בפרק הראשון של המאמר, בעזרת שימוש ב"הכללה לטרנספורמציית לורנץ", ראינו כי: סיכום השפעת ווקטורי עיקום המרחב על נקודת ריק כמעט מוחלט, שמסתה שואפת ל – "0", מתקזזת עם השפעת הנקודה מנגד, כך שנקודת הריק מוחזקת/קשורה למרחב, במרכז הכובד (בשונה מתורת המיתרים) שלה, ב"שיווי משקל רופף". מכאן עולה שכול הפרעה קטנה יכול שתגרום לתחילת תנועה בכיוון כלשהו (להל"ן: "דעיכה ספונטנית"), במהירות המקסימאלית האפשרית, היא מהירת האור הרגעית במרחב בו קיימת הנקודה.
נובע מהנחת אחידות המרחב, שבכל מיקום חדש, אליו תנועה נקודת הריק הכמעט מוחלט, גם שם, יתקזזו הווקטורים: עיקום המרחב ונקודת הריק הכמעט מוחלט עצמה מנגד, והנקודה, שוב, תהיה מוחזקת ב"שיווי משקל רופף". מכאן, שללא התערבות חיצונית, התנועה תמשיך, באותה מהירות ובאותו כיוון, עד לאין-סוף (וריאציה קוונטית, עבור נקודות ריק כמעט מוחלט, לחוק ההתמדה של ניוטון).
למעשה קיבלנו שנקודת הריק הכמעט מוחלט הפכה לפוטון חסר מסה, כזה שלאחר שקיבל דחיפה ראשונית מינימאלית (קריסת סימטריה), ינוע, ללא התערבות חיצונית, לעד במהירות האור הרגעית במרחב החיצוני לו.
והרי לנו פוטון בעל אנרגיה וחסר מסה, הנע במהירות האור.
על מהירות הפוטון, כאמור בסוף פרק 23, יהיה סביר יותר להסתכל מנקודת מבט של מערכת הצירים החדשה, בה מהירותו, הזהה ל – "0" בזמן היווצרותו, תשאר – "0" גם כשמהירות האור/אוסילציה של המרחב בתוכו הוא נע תשתנה. כך, אנו הצופים, עם ביצוע תצפית, נראה את הפוטון, הנע במהירות "0" במערכת הצירים החדשה, כנע במהירות האור הרגעית, נכון למועד התצפית, במערכת הצירים שלנו.
פרק 29: מוליכות על
תופעה נוספת, מעניינת ומוזרה, עליה, בהבנתנו את המושג "נקודות ריק כמעט מוחלט" והשלכותיו, נוכל לתת את הדעת.
עם קירור חומר לטמפרטורה הקרובה לאפס המוחלט (כ – 273°c-), יורדות – עד לכמעט "0", זהותית – גם השפעות מסות המנוחה של האלקטרונים והחלקיקים היסודיים המרכיבים את החומר. כך שניתן להתייחס לכולם כנקודות ריק כמעט מוחלט.
מכאן, בהתאם לפרק הראשון של המאמר, ניתן להסתכל על כל אלקטרון כזה כנקודת ריק כמעט מוחלט בתוך מרחב אין סופי של נקודות ריק כמעט מוחלט, הנמצא בשיווי משקל רופף עם הסביבה. כך, שבהתאם לפרק הקודם 28), כול דחיפה קטנה שאלקטרון כזה יקבל (מפל פוטנציאלים עליו), יכול שתגרום לו לתחילת תנועה, שללא התערבות חיצונית, תמשיך, ללא התנגדות, במהירות האור, עד לאין-סוף (קצה העל מוליך) – והרי לנו על מוליכות.
כיוון ששווי המשקל הרופף זהה בכול הכיוונים, זרם מספר אלקטרונים, תחת דחיפה ראשונית קטנה (פוטנציאל), צפוי שיתחיל בתנועה, בקו ישר וללא הפרעה כלשהי, בכל שטח הפנים של העל מוליך, בהתפלגות שווה.
זאת בניגוד למוליך בטמפרטורת החדר, בו, בהנחת מוליך בעל התפלגות מסה אחידה, בקירוב, האלקטרונים שחווים רק את חלק המסה שבינם לבין מרכז המוליך, ככול שיכנסו פנימה יחוו מסה נמוכה יותר.
מכאן, בהתאם לנאמר כבר בפרק הראשון בחלק הראשון של המאמר, שככול שנתקרב למרכז המוליך, בשל המסה הנמוכה יותר, עיקום המרחב שחווה האלקטרון יהיה חזק יותר, כך שהוא יידחף החוצה, לעבר פני המוליך בעוצמה חזקה יותר (הכול בהזנחת המסה החיצונית לאלקטרון, שבשל היותה גדולה יותר, פועלת בכיוון ההפוך בעוצמה פחותה – דהיינו מקזזת רק במעט את אפקט הדחיפה החוצה).
מצד שני, את המוליך בד"כ מקיף גז כלשהו (אוויר) אשר מסתו נמוכה בהרבה ממסת המוליך הממוצעת ולכן עיקומו את המרחב, כמובן, גבוה יותר, כך שאלקטרון ש"ירצה" לצאת החוצה יידחף חזרה פנימה – דהיינו קיבלנו שהאלקטרון (הזרם החשמלי) יהיה מאין כלוא, ללא הפעלת מפל פוטנציאלים או חודים כלשהם הגורמים לריכוז אלקטרונים גבוה, לנוע אך ורק על פני המוליך.
פרק 30: תנועת הגל במרחב
לאחר שהגדרנו את המושג מסה כסופרפוזיציה של פונקציות הגל העצמיות (פרק 24), נפנה להבנת התקדמות גלים במרחב. ונטען כי גל הוא הפרעה הנראית כנעה במרחב.
כבר בתחילת חלק זה של המאמר, משקבענו את ראשית מערכת צירים החדשה על נקודת ריק כמעט מוחלט שרירותית (פרק 17), קיבלנו שמנקודת השקפה שקולה זו (פרק 23) אורך הגל האופייני לנקודת ריק כמעט מוחלט במסה קטנה (ראה פרק 19), בניגוד להשקפה בפרק הראשון של המאמר, הינו קטן, לפי היחס הישר למסה.
מכאן שנקודת הריק הכמעט מוחלט, במסה זניחה, הינה בעלת אורך גל עצמי קצר, עד כדי כמעט חוסר משמעות.

כיוון שבמערכת הצירים החדשה, הצופה B, שהינו בעל מסה גבוהה, נע במהירות האור – "C", לכול הכיוונים, כולל לעבר נקודת הריק, בעת ובעונה אחת, הוא – לאחר שחזית הראיה שלו "D" (איור מס' 15), הנאה במהירות "C", תגיעה למקור האור "A" – יראה את חלק התנודה העצמית של נקודת הריק הכמעט מוחלט (קטנה ככל שתהיה), הניצבת לכיוון ההתקדמות שלו (איור מס' 16), כגל במשרעת מקסימאלית "y", הנע לעברו במהירות קבועה – "v = "C (ראה גם פרק 16).

מכאן, שלא נזדקק עוד לתווך כלשהו לצורך מעבר הגל במרחב. כך שהמושג "אתר", אשר נולד, בין היתר, לצורך הסבר מעבר הגלים במרחב, בעניין זה, יהפוך למיותר.
פרק 31: סיכום לחלק ב'
בחלק זה, בהתייחס לתאוריה שנבנתה בחלק הראשון, שינינו את נקודת המבט/ראשית הצירים ממערכת צירים סמויה שמרכזה במרכז הכובד של המסה, למערכת צירים, טבעית יותר, שראשיתה ממוקמת על נקודות הריק הכמעט מוחלט/אור/קרינה אלקטרו מגנטית וראינו שנקודת השקפה זו מסבירה תופעות רבות נוספות.
בעיקרו של דבר קבענו ששתי נקודות ההשקפה שקולות, מבחינה פיסקאלית. כך שלצורך תיאור המציאות ניתן להשתמש בכל אחת מהן ואף בשתיהן בעת ובעונה אחת.
לקראת סוף החלק הגדרנו את המושג מסה, תוך הבנה שהמסה איננה עוד גודל יסודי של הטבע, כפי שנהוג לחשוב, אלה שהיא תלויה בגודל יסודי יותר – התאבכות אוסף פונקציות הגל המרכיבות את המרחב המוגדר.
מצוידים בהגדרה חדשה זו למסה, המשכנו ודנו בתנועתה במרחב, תוך הבנה כי הכדור הרב מימדי מאין קשור למרחב במרכזו הדמיוני. והסברנו, בעזרת תנועת מרכז המסה של נקודת ריק כמעט מוחלת את היווצרות הפוטון (יצור חסר מסה הנע במהירות האור), כמו גם את תופעת העל מוליכות.
לבסוף, בפרק האחרון של חלק זה, התייחסנו בקצרה לתנועת הגל במרחב.
.
חלק ג': הצעה לבניית מכונת זמן
פרק 32: בסיס תאורתי
כבר בסוף הפרק הרביעי של החלק הראשון הזכרנו את האפשרות, התיאורטית, לבניית מכונת זמן.
לצורך בניית מכונת זמן, נתייחס לעובדות שהוזכרו עד כה, בניהן העובדה שמהירות האור היא מהירויות: האוסילציה והרגעית המהירה ביותר האפשרית בטבע (ראה הערה לקראת סוף פרק 7).
אם כך כאשר מסה, בדרך "מחוכמת", תעבור את מהירות האור, כאמור המהירות האפשרית הגבוהה ביותר בטבע, נצפה כי תעבור ל"יקום תאום"/מקביל בו: הזמן זורם הפוך, המסה עולה עם קיטון במהירות (מכמעט – "∞" ל – "C"), מהירות האור היא המהירות הנמוכה ביותר האפשרית בטבע (לא ניתן לרדת מימנה), יש להשקיע אנרגיה בכדי להאט גוף נע וכיוצ"ב תופעות שמרביתן הפוכות לאלו המוכרות לנו.
מכאן שגוף שיעבור ליקום תאום כזה, בו הזמן זורם הפוך כאמור, באמצעות מהירות רגעית העולה על מהירות האור, ויחזור כעבור זמן מה, יחזור לזמן מוקדם מהזמן בו עזב. באמצעות ידיעת מהירויות הגוף והאור הרגעיות, ההפרשים שבניהם וקצב השינויים במהירויות האור, בשני היקומים, נוכל לחשב את הזמן המדויק בו יחזור הגוף (הפרש הזמנים).
כול שנותר לבניית מכונת זמן כזאת הוא להניע גוף במהירות הגבוהה ממהירות האור הרגעית.
לצורך זה נאיץ חלקיק בעל מסה (עצם, אדם) למהירות הקרובה מאוד למהירות האור. לאחר שיגיע אליה, נקטין, יחסית בפתאומיות, את מהירות האור, המהירות הרגעית המרבית. מתקבל כי החלקיק/אדם שהואץ עד לכמעט מהירות האור, ימשיך במהירותו הקבוע, שתהיה גבוהה ממהירות האור הרגעית החדשה המוקטנת, אז יעבור ליקום התאום/מקביל.
את הכיוון חזרה מהיקום התאום, כפי שתואר כבר בתחילת הפרק, נעשה באמצעות השקעת אנרגיה להאטת הגוף למהירות הקרובה מאוד למהירות האור. אז בשינוי לעלייה במהירות האור הרגעית, מהירות הגוף תהיה נמוכה ממהירות האור הרגעית והוא יחזור ליקום מימנו בא.
כאן אולי הצורך להעיר כי נראה שהתופעות שתיארנו קוראות כל הזמן ובאופן רציף. ביקום שעובר את נקודת שיווי המשקל, שם מהירות האוסילציה מקסימאלית, כאמור, והולכת ויורדת עם הזמן, חלקיקים שנעו במהירות הקרובה (מלמטה) למהירות האור, ללא השקעת אנרגיה להאטה, ימשיכו באותה מהירות שתהפוך לגבוהה ממהירות האוסילציה הרגעית המוקטנת והם, לאחר שעברו את המהירות המקסימאלית הרגעית בטבע (ראה גם פרק 7 בחלק הראשון), יעברו ליקום תאום.
ברור שתופעה דומה, אך הפוכה, קוראת גם ביקום התאום/מקביל: חלקיקים שנעו במהירות הקרובה (מלמעלה) למהירות האור, כאשר היקום התאום מתקרב לעבר נקודת שיווי המשקל, ללא השקעת אנרגיה להאצה, עקב השינוי לעליה במהירות האוסילציה הרגעית, ימצאו את עצמם במהירות הנמוכה ממהירות האור הרגעית המוגדלת ויעברו ליקום תאום – הדומה ליקום שלנו.
כיוון שהתופעות קוראות בו זמנית, באופן סימולטני ורציף, כמות החלקיקים, לאורך זמן (ביחס למספר אוסילציות גדול של מחזורי יקום), העוברים ליקום התאום ובחזרה, דומה, כך שלטווח הזמן הארוך לתופעה, בכללותה, השפעה זניחה.
הערה: באמצעות שימוש בתחזית התאוריה לעיקום המרחב לעבר המסה (פרק ראשון של המאמר) נציעה לצפות באורו של כוכב רחוק הצפוי, בהשפעת המסה של חור שחור סמוך לדרכו, להתעקם, אך לא להיבלע. אם נוסיף כי החור השחור שיבחר יהיה כזה שמהירות האור הרגעית בו תהיה נמוכה ממהירות האור ביקום החיצוני לו, יתקבל כי: אור הכוכב העובר את מהירות האור הרגעית במרחב החור השחור יעבור ליקום תאום. כך, למרות שאור הכוכב צפוי היה להתעקם בהשפעת עיקום המרחב של החור השחור, הוא ימצא כנבלע/נעלם.
פרק 33: דוגמה מספרית
בדומה לפרדוקס התאומים שהוזכר כבר בפרק הרביעי של חלק א' של המאמר, נתייחס לשני תאומים. הפעם אחד התאומים יכנס למכונת זמן, כאמור בפרק הקודם, ויואץ למהירות של כ- 99.999999999819% ממהירות האור, אז יעבור ליקום התאום. בהתאם למקדם לורנץ (ראה התייחסות לטרנספורמציית לורנץ בפרק הראשון של המאמר), בהתעלם מהזמן הדרוש להאצה, יתקבל כי: בעוד שעוברת שנה שלמה על האח התאום שנישאר בכדור הארץ, דקה בלבד עוברת על האח במכונת הזמן – (מקדם לורנץ = [0.5^{2^(v/c) – 1}] / 1}).
לאחר שהאח עבר ליקום התאום, נאט אותו, תוך השקעת אנרגיה, לצורך חזרתו ליקום מימנו הגיע, למהירות הגבוהה ממהירות האור בכ – 0.000000000181% (בהנחה שהיחס זהה – דקה שעוברת עליו במהירות זו שווה לשנה על פני כל אחד מהיקומים התאומים), לפרק זמן של כ- 11 דקות לצורך העניין, אז יחזור ליקום מימנו בא והתאומים יפגשו.
נקבל כי על האח התאום שהיה במכונת הזמן, במשך המסע, עברו כ – 12 דקות. בעוד על זה שנישאר בכדור הארץ עברו כ- 12 שנים. כיוון שהאח בילה 11 דקות במכונת הזמן ביקום התאום, שם הזמן נע בכיוון ההפוך, שהם כ- 11 שנים ביקום מימנו בא, הוא יחזור, תוך 12 דקות כאמור, צעיר בכ- 10 דקות (1 דק' – 11 דק'), לזמן המוקדם בכעשר שנים (1 שנה – 11 שנים) מהתאריך שעזב.
הערה: "פרדוקס התאומים" עצמו, כפי שהוזכר כבר בפרק הרביעי של החלק הראשון, למעשה, מהווה מכונת זמן חד כיוונית (לעתיד בלבד). תאום שיסע לגלאקסיה הקרובה "אנדרומדה", מרחק של כ- 2 מיליון שנות אור לכיוון, במהירות הקרובה למהירות האור, יזדקן במהלך המסע הלוך ושוב (סה"כ כארבע מיליון שנות אור) בכ- 50 שנה, לצורך העניין. בעוד על כדור הארץ, במהלך המסע כולו, עברו כ- 4 מיליון שנים.
דהינו: במהלך המסע התאום עבר כארבעה מיליון שנים קדימה בזמן.
פרק 34: כיוון ועוצמת זרימת הזמן (פרדוקס הסבתא)
בהתאם לפרדוקס הסבתא, אם נעבור 100 שנה אחורה בזמן, נהרוג את הסבתא שלנו, אז במידה והרגנו אותה טרם לידת אימנו, לא ניוולד ולכן לא נוכל לעבור לעבר ולהרוג את הסבתא שלנו. לכן הסבתא לא מתה, כן עברנו לעבר, הרגנו את הסבתא שלנו ואנחנו לא קיימים, לא הרגנו את הסבתא… וכן הלאה מתקבלת לולאת זמן סגורה.
אז מה, אם כן, בעצם קורה.
כבר בסוף הפרק הרביעי של החלק הראשון הזכרנו את האפשרות להתייחסות לזמן כגודל ווקטורי, בעל עוצמה וכיוון, בדומה למרבית הגדלים האחרים בטבע. לאחר מיכן הזכרנו כי כיוון ועוצמת זרימת הזמן תלויה במסת היקום ובמהירות האוסליציה – המקבילה למהירות האור (בחלק ד', הבא, נדבר על גורם תלות נוסף – כיוון האוסילציה, אם להתפשטות או להתכווצות).
אם נתייחס לזמן, בדומה למי נחל זורמים, כגודל ווקטורי הזורם בכיוון השינוי המקסימאלי (מפל המסה או הגרדיאנט) של פונקציית המסה במרחב בו הוא זורם (גרדיאנט פוטנציאל כוח המשיכה לפי המרחב, במקרה של מי נחל זורמים), נקבל כי כאשר ההפרעה קטנה בזמן (הריגת הסבתא או פציעתה בלבד אחרי לידת אימי), בד"כ, היא תסתדר כעבור זמן קצר ותחזור לזרימת הזמן קודם להפרעה (דומה לאבן קטנה שמפריעה את מהלך הזרימה הסדיר של הנחל, שבד"כ יחזור לזרימה רגילה לאחר מרחק מה מהאבן).
אך אם ההפרעה משמעותית יותר, כפי שהזכרנו בתחילת הפרק, הרגנו את הסבתא טרם לידת אימנו (משול לאבן גדולה בערוץ הנחל), משמעותה יכול שתהיה עוצמתית בהרבה, לתקופת זמן ארוכה יותר ואף יכול שתגרום לכאוס (אי סדר) – תופעה הידוע גם בשם "אפקט הפרפר" – לתקופה ובמרחבים רחוקים, אולי אף ביקומים מקבילים.
למעשה, משהרגנו את הסבתא טרם לידת אימנו, עברנו ל"מציאות מקבילה", אחת מיני רבות, שסביר שיתאחדו, כולם, למציאות אחת בלבד (או נדיר יותר יתבדרו לכאוס), רק לאחר זמן רב. בזמן הביניים, ורק בו, אפשרי שהסבתא מתה, או מתה חלקית, בעוד אני חי מלא או חלקית (האבן הגדולה חוסמת את המים בעוד חלק קטן מהם ממשיכים בזרימה רגילה כבר במרחק קצר מאוד לאחריה).
לאחר זמן ארוך מספיק, כאמור, המציאות המקבילה סביר שתתאחד עם הקודמת והשפעת רצח הסבתא תתפוגג. לדוגמה: במציאות הקיימת, משפחתי, לאחר מותי, הושמדה כולה במלחמת העולם השנייה. כך שלא משנה עם הייתי קיים והולדתי צאצאים או שלא, לאחר איחוד המציאויות המקבילות, לא קיימים בעולם צאצאים שלי.
הזכרנו, גם אם במילה אחת, את האפשרות שהמציאות תתבדר לכאוס למספר מציאויות מקבילות: אחת בה אני קיים והסבתא לא, אחרת בה הסבתא קיימת ואני לא, שלישית בה שנינו קיימים, נוספת בה שנינו איננו קיימים וכול אפשרות של חלקי קיום ביניהם, כשכול אחת מהאפשרויות יכול שתתבדר לאפשרויות רבות נוספות. מתקבל, כעבור זמן ארוך מספיק, אי סדר, כאוס, אפקט הפרפר.
לאחר שסיימנו, למעשה, את הדיון במכונת הזמן עצמה, ניראה כי מן הראוי הוא שהחלק הבא של המאמר (חלק ד') ידון בהשלכות התאוריה עליה היא מתבססת (היקומים התאומים).
פרק 35: סיכום לחלק ג'
בחלק זה השתמשנו בחלק בסיסי מתוצאות התאוריה שהוצגה בחלקים הקודמים לצורך הצגת הצעה לבניית מכונת זמן, הכוללת דוגמה מספרית, ובחנו חלק מההשלכות התאורטיות.
לקראת סוף החלק (פרק 34) הצגנו את "פרדוקס הסבתא", בעזרתו הסברנו את כיוון ועוצמת זרימת הזמן, כווקטור הגרדיאנט, לפי המרחב, של המסה.
.
חלק ד': מהשלכות תאוריית התאומים
פרק 36: היקום מורכב בעיקר מחומר או איפה האנטי חומר ?
בהמשך ישיר לפרק 32 שבחלק הקודם, ניראה שאנטי חומר יתנהג בדיוק הפוך מהתנהגות החומר, דהינו: ביקום שעבר את אזור פני כדור שיווי המשקל ("O"), בזמן שחומר מימנו עובר ליקום התאום, אנטי חומר עובר מהתאום אליו. וביקום שעבר את אזור הקצה (X1 או X2, ראה איור 9), לעבר אזור שיווי המשקל, בזמן שאנטי חומר עובר מימנו ליקום התאום חומר מהתאום עובר אליו.
נסתכל, בפירוט יתר, סביב אזורי הקצה. בקצה מהירות האוסילציה, היא מהירות האור כאמור, רגעית, שווה ל- "0". מכאן שלאחר שעברנו את הקצה, כמעט כול החומר והאנטי חומר ביקום נעים במהירות האור – "0". דהינו: עם עליה קטנה במהירות האוסילציה/האור, כמעט במיידית, מרביתו המכרעת של האנטי חומר יעזוב את היקום ויעבור לתאום ובאותו הזמן מרביתו המכרעת של החומר יעזוב את התאום ויעבור ליקום שלנו (לצורך הבהירות נדגיש כי: בזמן שהיקום בהתרחבות התאום בצמצום/התכווצות וכן כשהיקום סביב פני כדור שיווי המשקל התאום סביב הקצה וההיפך, בהתאמה).
אם כך, נראה שתופעת האוסילציה של היקומים המקבילים יעילה בהסבר מיעוט האנטי חומר ביקום הנצפה אשר עבר במרביתו, בזמן שהיקום היה בתחילת ההתרחבות (לפי האפשרות השנייה בפרק 11), סביב הקצה, (נקודה X1 באיור מס' 9), ליקום התאום.
פרק 37: קווארק up וקווארק down – יקומים "שזורים"
נניח שהיינו יכולים לעזוב את היקום שלנו, להסתכל עליו מבחוץ ולהיות גדולים מימנו בכ- 20 סידרי גודל (בדומה לסדר גודל תת אטומי ביחס לקלאסי). אם, בתנאים אלו, נסתכל על היקומים התאומים ממרחק גדול מספיק, נניח אותם 20 סידרי גודל מקוטר היקום רחוק, השפעת כוח כבידתם שתימדד, ביחס לכוחות האחרים, למעשה, כמעט שתתאפס ונראה את זוג היקומים כשני חלקיקים שזורים קטנים מאוד, שכאמור בפרק הקודם, כשהאחד בהתרחבות השני בהתכווצות וההיפך.
כאן, מן הראוי להוסיף כי: כפי שנטען כבר בפרקים 8 ו- 26, בהסתכלות על היקום מרחוק מספיק, כ- 20 סדרי גודל רחוק כאמור, יכול שבהמצאות תנועות סביב או לאורך צירים ו/או קואורדינטות נוספות, או בדרך של כוחות נוספים, יוסברו תופעות קוונטיות נוספות, כגון: הספין הקוונטי וכיוצ"ב.
טרם נעבור לפרק הבא, ראוי להוסיף כי היקום יכול שימצא, אם במצב של צמצום או התרחבות, ביחס לפני כדור שיויי המשקל, באחת משתי האפשרויות: בין פני כדור שיווי המשקל והחוץ (נסמן ב- up) או בין פני הכדור והפנים (נסמן ב- down), והרי לנו תכונה קוונטית הנגרמת בשל האוסילציה פנימה והחוצה לאורך הרדיוס "r" (ראה פרק 26).
פרק 38: יקומים תאומים "שזורים" או רביעייה "שזורה" ?
בפרק מס' 5 דיברנו על שתי אפשרויות למצבים של התרחבות היקום, האחת מפנים הכדור לעבר שטח הפנים שלו, השנייה מפני כדור שיווי המשקל והחוצה. ובפרק 6 הוספנו שתי אפשרויות למצבים של צמצום היקום, מהחוץ לעבר פני הכדור או מפני הכדור לעבר מרכזו – סה"כ התקבלו ארבע אפשרויות שונות.
בנוסף, בהתאם לאותו פרק 6, עבור צופה חיצוני, יקום הנמצא בכל אחת משתי אפשרויות הצמצום נראה כחומר ויקום, בסדרי גודל קוונטיים, הנמצא בכל אחת משתי אפשרויות ההתרחבות, נראה כאנטי חומר. וכן, בהתאם למסקנה מהפרק הקודם (37), שתיים מהאפשרויות (כלפי חוץ ביחס לפני כדור שיווי המשקל) במצב up ושתיים (כלפי פנים ביחס לפני כדור שיווי המשקל) במצב down. מכאן שלמעשה, עבור הצופה החיצוני בלבד, מתקבלים ארבעת היקומים השזורים הבאים: האחד חומר (צמצום) up (מעבר לפני כדור שיווי המשקל), השני חומר down (צמצום בתוך פני כדור שיווי המשקל), השלישי אנטי חומר (התרחבות ביקום בסדרי גודל קוונטיים) up, והאחרון אנטי חומר down (המצב הנוכחי ליקום שלנו) – סה"כ התקבלה רביעיית יקומים שזורה.
לאחר שבפרק זה עסקנו ברביעייה השזורה מנקודת מבטו של צופה חיצוני, בפרק הבא נעסוק ברביעייה מנקודת מבטו של צופה פנימי – ונתמקד במעבר חומר/אנטי חומר בין מרכיביה.
פרק 39: הרביעייה ה"שזורה" – מבט מבפנים
כאמור, בפרק הקודם, עסקנו ברביעיית היקומים השזורים מנקודת מבטו של צופה חיצוני. עתה נסתכל על הרביעייה מנקודת מבטו של צופה החיי על גבי אחד מהרביעייה.
צופה פנימי כזה יכול שיחייה על אחד מבין הרביעייה הבאה:
- יקום בהתפשטות מהפנים לעבר פני כדור שיווי המשקל – במקרה כזה מרבית האנטי חומר, באזור הקצה "X1", עזב – כך שהיקום מורכב מרביתו מחומר.
- יקום בהתפשטות מפני כדור שיווי המשקל כלפי חוץ – במקרה כזה מרבית החומר, בסביבת פני כדור שיווי המשקל "O", עזב (או הגיב עם אנטי חומר, פרק מס' 46) – כך שהיקום מורכב מרביתו מאנרגיה.
- יקום בהתכווצות מהחוץ לעבר פני כדור שיווי המשקל – במקרה כזה מרבית החומר, באזור הקצה"X2" , עזב – כך שהיקום מורכב מרביתו מאנטי חומר.
- יקום בהתכווצות מפני כדור שיווי המשקל כלפי פנים – במקרה כזה מרבית האנטי חומר, באזור פני כדור שיווי המשקל "O", עזב (או הגיב עם חומר, פרק מס' 46) – כך שהיקום מורכב מרביתו מאנרגיה טהורה.
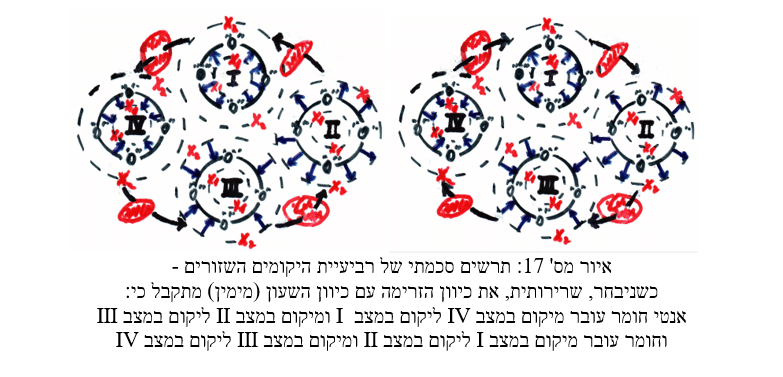
עוד עולה מהכללת מסקנת סימטריית המעבר חומר-אנטי חומר ואנרגיה בין היקומים התאומים (פרק 36), שקיימת גם סימטריית מעבר בין כל הרביעיה השזורה (ראה איור מס' 17), כך שבסה"כ כרבע (25%) מהמסה הכוללת (כולל אנרגיה) של הרביעייה, בכול זמן נתון, נמצאת בכל אחד מהם. דהינו: סה"כ סכום החומר, האנטי חומר + אנרגיה ביקום שלנו ובכל אחד מהרביעייה, צפוי שיהיו יחד, בממוצע לאורך זמן, כ- 25% – או כמות החומר, האנטי חומר + אנרגיה החיצוניים ליקום ולכן אינם ניתנים לצפייה, צפוי שתהיה בסביבות 75% – יחס של 1 : 3. התייחסות לתופעת ההשמדה העצמית, לאנרגיה טהורה, של חומר ואנטי חומר נפגשים והשלכותיה – בהמשך, בפרק 46.
התקבל כי ביכולתה של "תורת הכדורים" להציע הסבר לסדר גודל כמות ה"חומר האפל" ביקום. ובה בעת, באמצעות מצבו הנוכחי של היקום בהתרחבות, הנוכחית, מהפנים לעבר נקודת שיווי המשקל (פרק 11), גם ל-"האנרגיה האפלה" (ראה סוף פרק 11 – סעיף לאחר הניסוי ופרק 46, כאמור).
פרק 40: מטען/כוח הצבע
היקום בו אנו חיים (איור 17 מצב מס' Ⅰ), כאמור בשני הפרקים האחרונים, הוא אחד מרביעייה שזורה. מכאן ששלושת המצבים הווירטואליים האחרים (Ⅲ, Ⅱ ו- Ⅳ) צריך שיהיו מאוזני כוחות אתו. בהנחה שהכוח שמפעיל הייקום הוא ניטרלי (לבן), ללא השפעה חיצונית לרביעייה, גם הכוחות הפיקטיביים שמפעילים שלושת המצבים הווירטואליים האחרים מנגד צריך שיהיו ניטרליים.
דהינו: נחוץ לנו כוח, לאיזון הכוח הניטראלי שמפעיל היקום – הפועל בשלושה אופנים שונים: אדום, ירוק וכחול, בצורה שסך סכומם יהיה תמיד ניטראלי, לבן. והרי לנו שהכוח "החזק" הניטרלי (לבן) שמפעיל היקום שווה לסה"כ כוח מטען הצבע הניטרלי, גם הוא, מנגד.
התקבל, ש"תורת הכדורים", בשילוב תאוריית היקומים התאומים, מצליחה אף בהסבר חלק נוסף מהתאוריה הסטנדרטית של הפיסיקה.
פרק 41: ספין
באיור מס' 17 הנחנו את כיוון זרימת החומר והאנטי חומר, שרירותית, עם כיוון השעון (מימין). אך עם כול ביצוע מדידה על הרביעייה השזורה סביר שנקבל, בהתפלגות שווה, זרימה כנגד כיוון השעון (איור 17 – שמאל) ועם כיוון השעון (בסיכוי של 50:50). והרי לנו שתי אפשרויות שונות, תלויות מדידה, לספין המערכת (1/2+, 1/2-).
כאן, לדעתנו, ראוי לתת את הדעת להארה שבפרק 4 הקובעת כי קיימות אפשרויות סבירות פחות להתפתחות הזרימה (שם פונקציית הגל), כך שבכל נקודה קיימת אפשרות, אם כי בסבירות נמוכה, העולה בהדרגה עם הקירבה לפני כדור שיווי המשקל, שהיקום יעבור, בצורה לא רציפה (קפיצה קוונטית), לכל אפשרות אחרת מאלו המוצגות באיור מס' 17. מתקבל כי קודם ליקום במצב של התרחבות מואצת, מפנים כדור שיווי המשקל לפניו, כפי מצב היקום כיום, היקום יכול שהיה בכל אחת משלושת האפשרויות האחרות (לדוגמה: בהתרחבות מואטת), או אף במקום אחר באפשרות הנוכחית.
כאן ראוי, אולי עוד להוסיף, על משמעות פני כדור שיווי המשקל כרמת האנרגיה הקוונטית של נקודת הריק הכמעט מוחלט. מכאן שגם מעברי אנרגיה קוונטית, כמובן, שאפשריים, אם כי בסבירות נמוכה מאוד. מעבר אנרגיה שכזה משנה את רמת האנרגיה של פני כדור שיווי המשקל, מתחילה תנועה סביב פני כדור משקל חדש, ונפלטת/נקלטת אנרגיה אל מחוץ לכדור (היקום) או לתוכו.
פרק 42: פונקציית הגל וגדלים אחרים
בהמשך ישיר לפרק האחרון, גם פונקציית הגל עצמה, בדומה למצב up או down, לספין, לצבע וכיוצ"ב, הינה תופעה קוונטית, תלוית צופה. עבור צופה מספיק רחוק ומספיק גדול, בסדרי גודל כמו שהוזכרו בפרק 37 – חלקיק שלצופה קרוב ובסדר גודל דומה ניראה כקלאסי יראה כקוונטי. דהינו: פונקציית הגל איננה אבסולוטית, גם היא, כמו הגדלים האחרים, תלוית צופה.
מכאן, בהתאם להגדרת המסה, המתבססת על סופרפוזיציה של פונקציות גל (פרק 24), גם המסה וכמובן גם האנרגיה וכיוצ"ב גדלים קשורים – הם, כולם, גדלים התלויים בנקודת מבטו של הצופה.
למעשה, פרק זה מספק הוכחה נוספת לעיקרון האינווריאנטיות, העולה מפרקים 9 ו- 10 שבחלק הראשון של המאמר. ומתקבל כי: כל צופה, בכל יקום שהוא, גדול או קטן בלפחות 20 סידרי גודל, הנמצא באותה נקודה באוסילציה, ימדוד את אותה מהירות האור וכן את אותם התופעות הקוונטיות, הגליות והקבועים הפיסיקאליים האחרים. והכול ללא תלות בגודלו האבסולוטי של היקום.
פרק 43: תמונת היקום – הרביעייה השזורה
בפרק מס' 41 הסתכלנו על הרביעיה "השזורה" מקרוב או מיתוך אחד מארבעת היקומים המרכיבים אותה – אשר לצופה מרחוק נותנת את נקודת המבט הקוונטית. דרך נוספת לתאר את הרביעייה שבאיור 17 – הפעם במבט מרחוק – היא כענן פונקציית גל, המתפתח עם הזמן בין הקצוות – X1 ו- X2, כאשר פני כדור שיווי המשקל – "O", מהווה את מרכז הכובד של התנועה (רמת האנרגיה הקוונטית). ובתוך, מחוץ או במעורב עם ענן היקום נמצאים שלושת ענני חברי הרביעייה הווירטואליים הנוספים: אדום, כחול וירוק (ראה איור מס' 18). בנוסף, נזכיר שקיבלנו ששניים מהרביעייה במצב up ושני האחרים במצב down ושניים מהווים חומר כששני האחרים מהווים אנטי חומר – סה"כ ארבעת האפשרויות (פרק 39).

בהנחה שהיקום (בכתום) מהווה את מעטפת הרביעייה, משנבצעה מדידה/תצפית דרך הציר/מישור – "M", היות ושלושת ענני הרביעייה האחרים (אדום, כחול וירוק), המעורבים האחד בשני, אינם יכולים להימדד כחצי ענן/חלקיק/קווארק, סביר שיסתדרו, באופן אקראי, כך ששניים מהם יהיו למעלה/מימין לציר/מישור המדידה והשלישי למטה/משמאל, או ההיפך. אם נניח, בשונה מהתמונה שהוצגה בפרק 41, שמטען הרביעיה נקבע ע"י עוצמת אי הסימטריה במיקום שלושת חברי הרביעייה ביחס לציר/מישור המדידה "M", בד"כ נקבל שמטען הרביעייה הכולל יהיה: 1+ או 1-.
הערה: ברור שבסיכוי קטן יותר קיימות גם האפשרות ששלושת ענני הרביעייה האחרים (פרט למעטפת) יסתדרו באותו צד של ציר המדידה "M". במקרים כאלו נקבל שמטען הרביעייה הכולל יהיה, גם הוא, פי שלוש ממטענה באפשרות הסבירה יותר.
הערה: במקרה של קפיצה אנרגיה קוונטית, כמתואר בסוף פרק 41, נקבל כי מצבם הקוונטי (ספין, מטען, צבע וכיוצ"ב) של כול ארבעת חברי הרביעיה השזורה ישתנו סביב רמת האנרגיה (פני כדור שיווי המשקל) החדשה.
פרק 44: חור שחור, האם נקודה סינגולארית או מעבר פאזה ?
כבר מתחילת המאמר התייחסנו לשלושת המושגים: נקודת ריק כמעט מוחלט, היקום וחור שחור כמעט בנשימה אחת. מאיור מס' 18, בפרק הקודם, ניתן לראות כי: במרכז החור השחור, בנפח אפסי, נמצאים מרכז הכובד של המסה והאנרגיה, כשענני פונקציית הגל של הרביעייה השזורה מרוחים סביב. מכאן ניתן לשער שקיימת שם סינגולאריות.
הזכרנו כבר מספר פעמים, בפרקים קודמים של המאמר, כי גוף הנע במהירות הקרובה למהירות האור הזמן העצמי שלו מתקצר ביחס לצופה חיצוני, וכן, עבור הצופה החיצוני, מתקצר המרחב (האורך).
אם נתייחס גם לעולה מתורת היחסות הכללית כי: תאוצה שוות ערך לכבידה (אדם הנימצא בחללית לא יוכל לדעת האם החללית היא זו שמאיצה או שהוא תחת השפעת כבידה), נקבל שגוף המאיץ עד למהירות הקרובה למהירות האור, למעשה מחליף, מרוויח זמן ע"ח הפסד מרחק (מרחב). את החלפת זמן-מרחק זו, של גוף העובר את אופק האירועים של החור השחור (נופל לתוכו), נוכל לתאר כהמרת קואורדינטות של מרחב לקואורדינטות של בזמן.
נחזור לסינגולריות לכאורה.
כבר בפרק 12 שאלנו את השאלה: האם ניתן להגדיר את המרחב, במקום באמצעות מערכת הקואורדינטות המוכרת לנו, הכוללת שלוש קואורדינטות של מרחב ואחת של זמן, כמרחב הכולל שלוש קואורדינטות לזמן ואחת למרחב. נראה כי במרכז החור השחור, כמו גם במקרה של תאוצה למהירות הקרובה למהירות האור, יהיה המקום המתאים להשתמש במערכת קואורדינטות חדשה זו.
עם השימוש במערכת קואורדינטות כזו מתקבל כי: גוף הנכנס לחור השחור, המקטין, בהדרגה עם הנפילה, את נפח המרחב בו הוא מרוכז, בשלוש קואורדינטות המרחב המוכרות לנו, עד לנפח נקודתי, (מימדי מרחב אפסיים), למעשה, ממיר הפסד מרחב זה בנפח כדור תלת מימדי (שלוש קואורדינטות) של זמן וקואורדינטה אחת למרחב. כך החומר, המסה והאנרגיה, למעשה, מתפזרים במרחב כדורי תלת מימדי, הולך ומתרחב עם הנפילה לחור השחור, של זמן והסינגולריות נעלמת.
דהיינו: קיבלנו שמרכז החור השחור הוא נקודת "מעבר פאזה", בין מרחב לזמן – לא עוד נקודה סינגולארית.
פרק 45: "חור לבן"
ממשמעויות הפרק הקודם: חלקיקי גוף/עצם שנופל לחור השחור מתפזרים בכדור זמן בנפח עצום, עד כדי צפיפות זמן ממוצעת אפסית. דהינו: כדי לנצל, ככול שהם קיימים, "חור תולעת"/"גשר איינשטיין-רוזן", לצורך מעבר בזמן, יהיה צורך לאסוף את כול חלקיקי החומר שהרכיבו את העצם, אשר, עם הנפילה, התפזרו בזמן, בחזרה לכדור זמן מצומצם (מימדי זמן אפסיים). רק אז ניתן יהיה לעבור לצד השני של הגשר ולצאת בחזרה, כיחידה שלמה, בשלוש קואורדינטות של מרחב ואחת לזמן, למיקום אחר, בזמן ובמרחב, דרך ה- "חור הלבן".
מעשית, ספק רב אם תהיה יכולת כזאת, ולו רק תאורטית, לאסוף את כול המידע שהתפזר בכדור הזמן התלת מימדי לצורך העברתו, דרך הגשר, בשלמות.
בעניין זה ראוי להזכיר את הדיון בפרק השלישי של החלק ראשון של המאמר, בו דיברנו על כך שנקודת ריק כמעט מוחלט במסה אפסית, בשל כך שאורך הגל האופייני של התדירות העצמית שלה גדול מאוד, פונקציית הגל שלה מפוזרת במרחב תלת מימדי גדול מאוד. בדרך הפוכה, ניתן להסתכל על חור שחור במסה גבוהה. חומר שיפול לחור השחור או אף החור השחור עצמו, ככול שמסתו גבוהה יותר, יתפזר בנפח זמן גדול יותר (מרחב קטן יותר) מתקבל מאין "חור זמן לבן".
לכן, אם נניח שבדומה לחורים שחורים במרחב קיימים גם חורים זמן שחורים (כדור זמן גדול המרוכז בנקודת זמן אפסית), ניתן יהיה להניח שהיציאה מחור זמן כזה תהיה דרך חור זמן לבן (חור שחור רגיל) – בדומה לחור התולעת בצד השני של גשר איינשטיין-רוזן.
האם מעברים אלו הם לא אותם המעברים בין היקומים התאומים, עליהם התחלנו לדבר כבר בפרק 32 ?
פרק 46: המקור ל-"אנרגיה האפלה"
כפי שהזכרנו כבר בפרק החמישי היקום שלנו נמצא בהתרחבות, מפנים הכדור התלת ממדי לעבר פני כדור שיווי המשקל (פרק 11). מכאן, לפי פרק 39, בסביבת "x1" (איור מס' 9) היקום איבד את מרבית האנטי חומר ונותר יקום המורכב מרביתו מחלקיקי חומר. עם הזמן, יותר ויותר אנטי חומר זורם מיקום מס' Ⅳ ליקום שלנו וחומר זורם מהיקום שלנו ליקום מס' Ⅱ (איור מס' 17). האנטי חומר הנכנס מגיב עם החומר הקיים והופך לאנרגיה טהורה – היא המקור לאנרגיה האפלה. כך קיבלנו שהאנרגיה האפלה, עד שהיקום יגיע לפני כדור שיווי המשקל – "O", עולה עם הזמן – בעוד, במקביל, המסה יורדת. שני שינויים המשפיעים באותו כיוון, להאצת מהירות ההתפשטות.
משיקולים דומים קל להבין שבנקודה "O", שם היקום, לאחר שאיבד כבר את מרבית החומר וממשיך לקבל אנטי חומר מיקום מס' – Ⅳ (איור 17), מורכב במרביתו מאנרגיה טהורה. אז מסתו וכוח המשיכה מתחזקים ומהירות ההתפשטות הולכת וקטנה, בהתאם.
ניתוח דומה ניתן לעשות בכל נקודות הקיצון האחרות ולקבל את הגורמים להאצת/האטת מהירות ההתפשטות. מסה הופכת לאנרגיה המאיצה את מהירות ההתפשטות ולאחר מיכן, כשעולה המסה על חשבון הירידה באנרגיה, כוח המשיכה מתחזק – דבר המקטין, במקביל לקיטון באנרגיה, את מהירות ההתפשטות וחוזר חלילה.
פרק 47: סיכום לחלק ד'
בפרקים 36 עד 46 דנו בהשלכות תאורטיות, קוונטיות וקלסיות, של "תורת הכדורים" יחד עם תאוריית היקומים המקבילים – עליה מתבססת מכונת הזמן שבפרק ג'. וקיבלנו הסברים טובים למיעוט האנטי חומר ביקום ולכמות החומר האפל ולבסוף גם הסקנו לגבי המבנה הכללי של היקום, החורים השחורים והלבנים – ככול שאלו קיימים.
לבסוף, בפרק האחרון של חלק זה, קיבלנו את חוק השימור המתאים ל-"אנרגיה האפלה" – עליה דיברנו כבר בפרק 11 של החלק הראשון.
.
חלק ה': ניסוי מוצע להוכחת התאוריה
הקדמה לחלק ה':
ניסוי זה, כרונולוגית, נכתב קודם לכתיבת חלקים ג' ו- ד' של המאמר (התאוריה מבוססת על "תורת הכדורים"). חלקים שהתגלו מאוחר יותר כעומדים בסטירה לדרך מדידת השינוי, עם הזמן, במהירות האור שמציע הניסוי. הסטירה, כמובן, נובעת מכך שככול שתאוריית הרביעייה השזורה נכונה, להבדיל מ"תורת הכדורים" עצמה, מתחייב מימנה שלא נוכל להפריד את חברי הרביעייה השזורה – לכן המסה שתימדד תהיה המסה הכוללת של ארבעתם, שבשונה ממסת כול יקום בנפרד, תיוותר קבועה בזמן. כך, דרך המדידה העקיפה שמציע הניסוי, למדידת השינויים, עם הזמן, במהירות האור באמצעות השינויים במסה (פרק 50), למעשה נופלת.
עדיין, ולמרות הסתירה כאמור, בחרתי להשאיר את פרק הניסוי, המוצע, כחלק מדרך החשיבה הכוללת השלמה של המאמר. אולי, גם, בתקווה שתמצא דרך למדוד את השינויים במהירות האור והמסה של כול אחד מארבעת היקומים השזורים בנפרד (על ניסוי מוצע מעודכן למדידת קצב שינוי מהירות האור לאורך תקופת זמן ארוכה בהמשך, לקראת סוף חלק זה).
פרק 48: סיכום קצר למאמר
בחלק הראשון: של המאמר (פרקים 1 עד 13): נוכחנו כי עיקום המרחב, כוח המשיכה ולמעשה תאוריה מאוחדת לחמשת כוחות הטבע הידועים (משיכה, חשמלי, מגנטי והכוחות הגרעיניים: החזק וחלש) כולם מתקבלים, בשילוב העולה מתורת הקוונטיים, כתוצאה ישירה מההנחה, המתבקשת, כי היקום מורכב מאין ספור נקודות ריק כמעט מוחלט, (כשבהמשך, בסוף החלק השני (פרקים 26 – 29) של המאמר, הבנו כי הן מאין קשורות למרחב במרכזם).
בהמשך החלק הראשון ראינו שאפיוני האוסילציות ההרמוניות של נקודות הריק הכמעט מוחלט סביב שיווי המשקל, במהירות תנודה "C", למעשה המהירות המקסימאלית האפשרית בטבע המשתנה, לאורך זמן – בין 0 בקצוות למקסימאלית, כמעט אין סופית, במרכז (פני כדור שיווי המשקל) – מגדירים את: החומר, האנטי חומר והחומר והאנרגיה האפלים – כפי שמוכרים לנו.
כן, הזכרנו את שעולה מתורת היחסות, כי ככול שמהירות גוף מתקרבת למהירות האור, מסתו עולה והזמן העצמי שלו מתקצר (פרדוקס התאומים). בנוסף הוזכרו: הנוסחה הידועה – " E= M x C2" ועקרון האינווריאנטיות של חוקי הפיסיקה, ללא תלות בגודלו היחסי של היקום.
ניסינו, ככל הנראה ללא הצלחה יתרה, להציע ניסוי מחשבתי למדידת השינויים במהירות האור מאז הולדת היקום, עובר להיום ולעתיד, אך כל שקיבלנו היה הסבר חלקי לאנרגיה העצומה הנמדדת, הבלתי מוסברת, של הקוואזרים.
בחלק השני: (פרקים 14 – 31) שינינו את נקודת המבט/ראשית הצירים ממערכת צירים סמויה שמרכזה במרכז הכובד של המסה למערכת צירים, טבעית יותר, שראשיתה ממוקמת על נקודות הריק הכמעט מוחלט וקבענו שמבחינה פיסיקאלית שתי נקודות ההשקפה שקולות. כך שלצורך תיאור המציאות ניתן להשתמש בכל אחת מהן בנפרד ואף בשתיהן בעת ובעונה אחת. בהמשך נוכחנו, תוך הגדרת המושג מסה והתייחסות לתנועה של מרכז המסה, שנקודת השקפה נוספת זו מסבירה תופעות רבות נוספות, כגון: מהירות האור הקבוע בכל הכיוונים, עיקרון אי הוודאות, פוטונים, על מוליכות וכיוצ"ב. לבסוף, בפרק האחרון של חלק זה, התייחסנו בקצרה לתנועת הגל במרחב, מנקודת המבט של מערכת הצירים החדשה.
בחלק השלישי: (פרקים 33 – 35), בהתבסס על חלק מהידע שצברנו, אף הצענו דרך תאורטית לבניית מכונת זמן, כולל דוגמה מספרית, ובחינה חלקית של השלכותיה התאורטיות.
בחלק הרביעי: (פרקים 36 – 47), בהתבסס על תורת הכדורים ותאוריית היקומים התאומים – עליהם מתבססת מכונת הזמן שבחלק השלישי, קיבלנו הסברים טובים למיעוט האנטי חומר ביקום ולכמות ה"חומר האפל" ו– ה"האנרגיה האפלה" שבו והסקנו, כללית, לגבי מבנה היקום והחורים השחורים והלבנים, ככול שקיימים.
לאחר כל אלו (החלקים הראשון עד הרביעי של המאמר), ניראה כי עדיין נותרנו עם השאלה הפתוחה הגדולה מכולן: בהתבסס על כל שהוזכר, "איך והאם ניתן להוכיח שמהירות האור, כפי שחוזה התאוריה, אכן משתנה לאורך השנים".
פרק 49: הקשיים העומדים בפנינו
- לא נראה שקיימת, או לפחות לא נמצאה עד היום, דרך למדידה ישירה של השינויים, לאורך זמן, במהירות האור.
- גם אם תמצא דרך כזאת, יש למדוד את השינויים במהירות האור לאורך תקופת זמן ארוכה, מיליארדי או לפחות מספר מאות מיליונים של שנים.
–
פרק 50: פתרון הקושי הראשון
כדי לפתור את הקושי הראשון וכיוון שדי ברור שנתקשה למדוד, ישירות, את השינויים, עם הזמן, במהירות האור, במקום מדידה ישירה, נציע דרך עקיפה. לצורך המדידה העקיפה, נעזר בנוסחה הידועה שהוזכרה – "E = M x C2" ונטען שמדידת השינויים במסת נקודת הריק הכמעט מוחלט (או אף אם היא בעלת מסה כזאת או אחרת), בהנחה שהשינויים, לאורך הזמן, באנרגיה שלה זניחים (מערכת סגורה), למעשה, הינה מדידה עקיפה אך שקולה.
דהינו: כעולה מהנוסחה ובהנחה שהשינויים, לאורך הזמן, באנרגיה זניחים, כאמור, השינוי במהירות האור הינו ביחס הפוך לשורש השינוי במסה. כך כול שנותר למדידת השינוי במהירות האור ולהוכחת התאוריה, למעשה, הינו מדידת שינויי המסה לאורך השנים.
פרק 51: פתרון הקושי השני
נותרנו עם הבעיה השנייה, שלכאורה, נראית קשה אף יותר מקודמתה.
כאמור, כפי שעולה מתורת היחסות, גוף הנע במהירות הקרובה למהירות האור מסתו עולה והזמן העצמי שלו מתקצר. או במילים אחרות – "ככל שמסתו של גוף גבוהה יותר הזמן העצמי שלו זורם לאט יותר" – והפוך הזמן העובר על צופה מחוץ למסה נעה זורם מהר הרבה יותר מהזמן ביחס לזה של צופה החיי עליה.
כך, כתלות בגודל המסה, לדוגמה: 100 מיליון או מיליארד שנים העוברים עלינו יכול שיהיו שקולים לחצי שנה העוברת על צופה הממוקם על המסה. מכאן שכשנמדוד את השינויים במסה שבדוגמה במשך תקופה של חצי שנה, למעשה, בהתאם לעקרון האינווריאנטיות, מדדנו את שינויי המסה, ביחידות זמן שלנו, למשך תקופה ארוכה הרבה יותר, העוברת על צופה החי על המסה.
הסבר לעיקרון האינווריאנטית: בהתאם לעיקרון, בדוגמה שלנו, שינויים, של – %X, במסות הגוף והיקום (או במהירויות האור) העורכים על המסה, לצורך העניין, תקופה של כחצי שנה, אצלנו, יכול שיהיו שקולים לשינויים דומים העורכים תקופה של כ – 100 מיליון או אף מיליארד שנים, כתלות ביחס המסות, כאמור.
פרק 52: הניסוי
כול שנותר הוא למצוא גוף בעל מסה גבוהה מאוד, כזה שהפרשי זרימת הזמנים עבור צופה הממוקם על המסה ואחר מחוץ לה יהיו גדולים ככול האפשר, עליו ניתן לבצע את המדידה. המועמד הטיבעי ביותר לצורך זה, באופן די ברור, הוא חור שחור.
לצורך המדידה, נבחר חור שחור או מערכות כוכבים כפולים שאחד ממרכביה הוא חור שחור בלתי נראה ונציע את המדידות הבאות:
- מדידה עקיפה של שינויי מסת החור השחור, באמצעות מעקב אחר השינויים לאורך פרק זמן של כחצי שנה, לצורך העניין, בעוצמת עיקום קרני האור של כוכב רחוק העוברות בסמוך לו (בדומה לניסוי עיקום המרחב שגורמת מסת השמש שבוצע להוכחת תורת היחסות).
- לחילופין, במערכת כוכבים כפולה שאחד ממרכיביה, כאמור, הוא חור שחור, נמדוד ישירות את השפעת השינויים במסת החור השחור, לאורך פרק זמן של כחצי שנה לצורך העניין כאמור, על הכוכב השכן.
.
פרק 53: תוצאות הניסוי
במידה ולאורך זמן, אכן יצפו, אם להגדלה או להקטנה, שינויי מסה, ישתמע מכך כי גם מהירות האור/האוסילציה של החור השחור משתנה עם הזמן – כפי שהתאוריה חוזה, כאשר, כפי שנטען, השינוי שיימדד במהירות האור צריך שיהיה ביחס הפוך לשורש השינוי במסה.
הערות:
- השינוי במהירות האור יכול שיהיה לעלייה או להקטנה. הכול בהתאם למיקום האוסילציה ביחס לנקודת שיווי המשקל: כאשר האוסילציה היא לעבר נקודת שיווי המשקל, מהירות האור בעליה (המסה בירידה) וכאשר האוסילציה עברה את הנקודה, אם לתוך כדור שיווי המשקל או החוצה לו, מהירות האור בירידה (המסה בעליה).
- תוצאה אפשרית: יכול שחלק, אולי אף חלק ניכר מכוכבי הפולסר, המשנים את עוצמתם בתדירות קבועה, יוסברו באמצעות שינויי מסתו של חור שחור או שכן כבד אחר, בלתי נראה.
.
לסיכום חלק זה (ה'), פרק הניסוי המוצע להוכחת התאוריה – שנים ספורות לאחר סיום כתיבתו, מצאתי לנכון שראוי להוסיף כי: לאחר שנתבקשתי, ע"י רבים, להציע ניסוי אפשרי למדידת קצב השתנות מהירות האור לאורך זמן ומאחר שהניסוי המוצע בפרק נפל, כאמור בהקדמה לחלק זה. בתחילת שנת 2023, ניסוי כזה, המבוסס על סוף פרק 11 בחלק הראשון של המאמר, אכן נכתב:
- לקישור להצעת הניסוי – לחץ.
- לקישור להצעת הניסוי בגרסה האנגלית – לחץ
- לקישור למצגת הרצאה להצעת הניסוי – לחץ.
.
אחרית דבר:
המאמר שבתחילה שם לעצמו כמטרה צנועה, את הניסיון למצוא דרך לאיחוד כוח המשיכה עם הכוחות האחרים הידועים כקיימים בטבע (פרק 1), למעשה, המשיך והיה לתורת כבידה (גאומטרית) קוונטית. התאוריה, שהמשיכה והתפתחה, הציעה, בדרך, הסברים (תאוריות מבוססות "תורת הכדורים") לתופעות רבות נוספות ואף ניסוי להוכחתה.
אני מאמין שאם ניסוח מתמטי מדויק של התאוריה, היא תפליא ותפתור עוד תעלומות מדעיות רבות, ותעלה עם הזמן, כמו כול תאוריה מדעית חדשה, שאלות נוספות שיהיו זקוקות, גם הן, למענה.